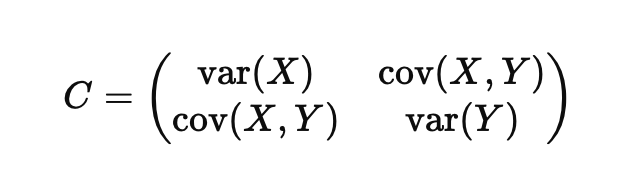共分散行列から固有ベクトルと固有値を計算するプロセスを直感的に理解するために、段階を追って説明します。幾何学的なイメージを持ちながら進めますね。
1. データのばらつきを捉える共分散行列
まず、データのばらつきを把握するために、共分散行列を計算します。共分散行列は、データの変数間の関係性を表現します。ここでは、異なる変数がどのように変動しているか(共変動)を示します。
- 共分散が正であれば、2つの変数は同じ方向に動きやすい(両方が増加または減少)。
- 共分散が負であれば、一方が増えると他方が減る傾向にある。
共分散行列は、こうした情報を行列形式で整理したものです。例えば、2つの変数の場合、次のようになります:
2. 固有値・固有ベクトルの計算の意義
共分散行列を使うと、データのばらつきの方向を見つけることができます。固有値と固有ベクトルを計算することの意義は、この方向を数値的に特定することにあります。
幾何学的に見た場合の解釈
- 固有ベクトル:
- これは、データの分散が最大になる「軸」を示します。幾何学的に言うと、このベクトルの方向にデータが最も広がっているということです。
- 固有値:
- これは、固有ベクトルの方向にどれだけの分散があるかを示します。固有値が大きければ、その方向に多くのデータが散らばっていることを意味します。逆に小さければ、あまり散らばっていないということです。
3. 計算の流れとイメージ
ステップ1: 固有方程式の導出
共分散行列から固有値と固有ベクトルを求めるために、固有方程式を使います。



この式は、固有値に対する固有ベクトルを求めるための方程式です。ここで解が得られるベクトルは、先ほどの固有値に対応する方向を示します。このベクトルの方向が、データのばらつきを最もよく説明する主成分の方向になります。
4. イメージのまとめ
- 共分散行列: データのばらつきの全体像を表す。
- 固有方程式: どの方向にデータが集約されているかを見つけるためのもの。
- 固有ベクトル: データのばらつきが最大になる方向。
- 固有値: その方向にどれだけのばらつきがあるか。
この流れを通じて、共分散行列から固有ベクトルと固有値を計算することは、データの構造を理解し、次元削減を行うための強力なツールとなります。
===
    |
    |
    |
"make you feel, make you think."
SGT&BD
(Saionji General Trading & Business Development)
説明しよう!西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である!平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである!「働かざること山の如し」。彼がただのニートと違う点はたった1つだけ!そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。