微分、積分とは何かについてわかりにくく解説してあげよう。
結論から言うと、
- 関数
- 微分
- 積分
の関係性が見えるようになる必要がある
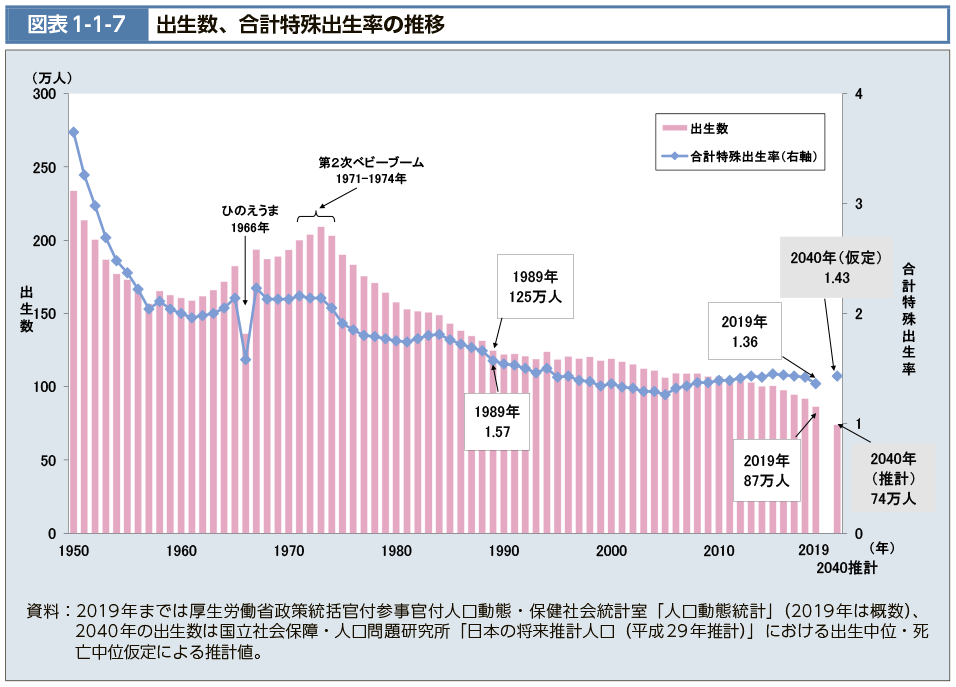
出生数グラフで言うと、この減り方が関数だ。右肩下がりになっている。そしてそれを「2019年〜2020年はどれだけ差があるか?」というズームアップの視点で見るのが微分だ。
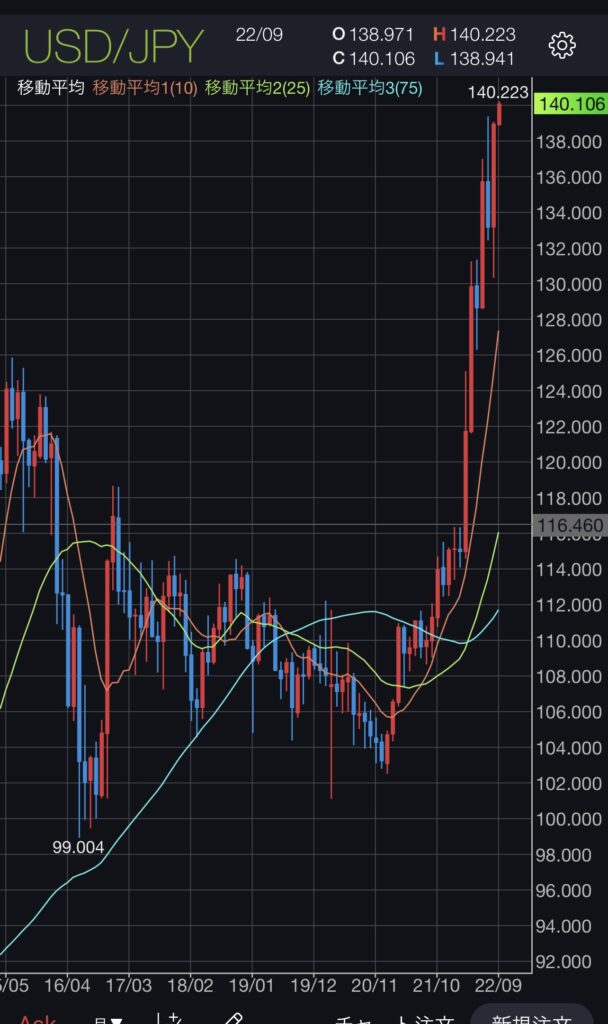
ちなみに、為替レートで言うと、最近の円安は微分的にエグい。
積分はそのグラフの下の範囲で、例えば1950年から2020年までの間を積分すると、まさにそれは累積の赤ちゃん出生数であり、すなわち人口になっていく。
この
- 関数
- 微分
- 積分
は面白くて、まず積分から行くと、積分というのはめちゃくちゃ極小の単位で見ていけば微分になる。要は積分値は微分値に支配されていることになる。
積分は、幾何的に捉えると面積なので「タテ✖️ヨコ」だがそのヨコを消失させるぐらい極小で見ていくとそれは「タテ」だけ見ているのと同じになり、それは結局微分。
さらに、微分も結局、
「どれだけ変化するか」
という概念であるが、それは元々の関数の形に支配されている。極小の単位で見ていくと、結局、それは関数。
「関数が微分を支配し→微分が積分を支配する」
という構図を見ることが重要。
さらに、A区間での積分と、B区間での積分の差を見た時、定義上、その増分というのは、
「関数の形状(タテ)✖️区間差分(ヨコ)」
であって、それを極小の単位で捉えたものは結局、微分である。
2010年度の貯金が100万、
2011年度の貯金が200万、
2012年度の貯金が300万
2013年度の貯金が3000万、
というケースにおいて、積分の変化を捉えると、2012〜2013では収入が急成長したのではないか、という推測が立つが、これが積分から微分を捉えるという考え方である。
相場でモノを考えたとき、
「同じ140円」
に到達するのであれば、
1週間で到達するのも、
1年で到達するのも、
同じく120円ラインで張ったならば同じことである。儲かる分は変わらない。むしろ、1週間で到達した方が早く儲かる。その意味で微分がエグい方がウハウハだ。
一方で、この二つのケースにおける、背後にある相場の構造は違う。
これが1年で到達するケースなら、上昇の形は緩やかになるから微分は緩やかになる。ただし、積分は厚くなることになる。
- 急上昇ケース 微分えぐい 積分薄い
- 緩やかケース 微分緩やか 積分厚い
ということになる。
関数の形が違う
だけで捉えていたものを、「積分が違う」と捉えてみると、実は結構、面白いことが見えてくる。これが数学を学ぶ効用でもある。きっと、数学が分からなければこのような視点を持って相場を捉えることはできないだろう。
例えば、以上のプロセスを「資金効率」という文脈で読み解く方法がある。株式市場で考えてみよう。
例えば短期筋が順張りする場合、その株が動意づく前に買ってた人を1とすると、その株を常に監視して上がり出す雰囲気を感じてまだ大して上がってない時に、勇気出して買う人を2として、その後完全に上がり出したのを確認してその株が次の日も、上がると思って買う人を3、その日の高値で買う人を4とすると、出来高として盛り上がるのは3~4の間。さらに乗っかるのを5、それより後で買う人を6とすると短期のつもりで3~4の間で買った人は良くて6の人に売って利益を出すことになり、短期間で金を稼いだという意味で資金効率は良いものの、1で買った人の膨大な利益には到底及ばない。しかし、1の段階で買ってる人は長期の人(資金効率は悪い)でしょうから、資金効率的なリスクを負っている。
積分で物事を考えると、市場構成要員の事情が見えてくるのである。
積分がわかると、微分もわかってしまい、関数の形もわかってくるので、そこから未来予測につなげることもできるのである。
===
    |
    |
    |
"make you feel, make you think."
SGT&BD
(Saionji General Trading & Business Development)
説明しよう!西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である!平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである!「働かざること山の如し」。彼がただのニートと違う点はたった1つだけ!そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。