ガチプロマーケティングマンが教える、数理モデリングの作り方と、「稼ぎ方」

一流データサイエンティスト・マーケターの西園寺貴文が数理モデリングについてどこで聞くこともできないオリジナルの話をしてあげましょう。

（こちらの記事も必見）

数理モデルはまず、大まかに以下のように分類できるでしょう。

①

線形か

（要素還元が可能）

非線形か

（カオス、ソリトン）

②

決定論的か

（一般的な方程式）

確率過程か

（マルコフ過程）

③

静的か

（数理計画化問題）

動的か

（微分方程式）

一応、これは数学概論です。

高校数学〜大学数学くらいがわかる人はなんとなくわかるでしょう。

①非線形だと、扱いが難しくなります。例えば、線形的な方程式を作った後に、「３次の項」を入れるなどして近似したりするのではないでしょうか。

②決定論的か、確率過程か、の折衷には伊藤の「確率微分方程式」があることをおさえておくと良いでしょう（確率微分方程式から勉強してしまうと早いです。金融工学への理解も早まります）。

③動的か静的かについてですが、動的なものは微分方程式、静的なものは数理計画問題（最適化問題・オペレーションズリサーチ等）などが該当します。

怪しい金融自己啓発本に騙されて・・・・

私は、「お金持ち」になりたくて、金融本・投資本をたくさん読んで、複利の概念に触れました。複利こそがお金持ちになる幅員であると。

しかし、ウォーレンバフェットのいうような「ゆっくり金持ちになる」というコンセプトが嫌だったのです。

そこで出会ったのが、インターネットマーケティングやコピーライティングの世界でした。ここには、投資よりも圧倒的に小資本から、高速回転で複利を回せる構図があります。

（私が今、マーケティングの仕事をしているきっかけです）

つまり、成約率を高めておいて、得られた成約・売上収益から広告再投資費用を捻出する、ということを繰り返していけば、どんどんお金が増えるというロジックです（1%に賭けるマーケターたち）。

基本的に、お金持ちになるというのはこういった非線形的な上昇を見つける、探すということを意味しています。その意味では、「数理モデリング」と密接に関係しています。

数理モデリングの詳細

数理モデリングは、現実世界の複雑な現象や問題を数学的なモデルを用いて理解し、予測・解析するプロセスです。以下に数理モデリングの一般的なステップを詳しく説明します。

問題の定義と理解: まず、対象とする問題や現象を明確に定義し、その背景や目的を理解します。どのような情報を得たいのか、どの種類のモデルが適切かなどを考えます。
モデルの選択: 問題の性質に基づいて適切なモデルを選択します。モデルは、数式や関数、グラフ、システム方程式などで表現され、現実の要因や相互作用を捉えるための道具となります。
変数とパラメータの定義: モデルを構築するために、関連する変数（要因や量など）とパラメータ（モデル内で調整可能な定数）を定義します。これによってモデルの特性や挙動が表現されます。
モデルの構築: 選択したモデルに基づいて、変数とパラメータを組み合わせて数式や方程式を構築します。モデルが複雑な場合は、代数、微分方程式、確率論などの数学的手法を使用してモデルを表現します。
初期条件と境界条件の設定: モデルが現実的な予測や解析を行うためには、適切な初期条件（モデルの初めの状態）と境界条件（領域の境界での挙動）を設定する必要があります。
モデルの解析: 構築したモデルを解析し、数学的手法を用いて解を求めたり、モデルの特性や挙動を理解したりします。解析の際には、代数的手法、数値計算、解析的解法などを利用します。
モデルの検証と調整: モデルが現実の現象を適切に表現しているかどうかを検証します。実際のデータとモデルの結果を比較し、必要に応じてモデルのパラメータや構造を調整します。
予測と応用: 検証が完了したら、モデルを使用して未来の予測や現象の理解を行います。モデルを通じて得られた知見を実用的な応用に活かすことが目指されます。
コミュニケーションと報告: モデリングの結果や洞察を他の人に伝えるために、結果を適切に可視化し、報告書やプレゼンテーションとしてまとめます。
繰り返しと改善: モデルが現実を十分に表現できるようにするために、繰り返しモデルの改善や修正を行います。新たなデータや洞察が得られる度に、モデルを更新して精度を向上させることが重要です。

数理モデリングは問題の種類や複雑さによってアプローチが異なる場合もありますが、上記のステップは一般的なガイドラインとして参考になるでしょう。数学的な専門知識と問題解決能力が求められるため、専門家の協力や適切なツールの活用が重要です。

四則演算の徹底理解の重要性

続いて、

数理モデリングは四則演算

（＋ー×÷）

に対する本質的な理解

が無いと考案できません。

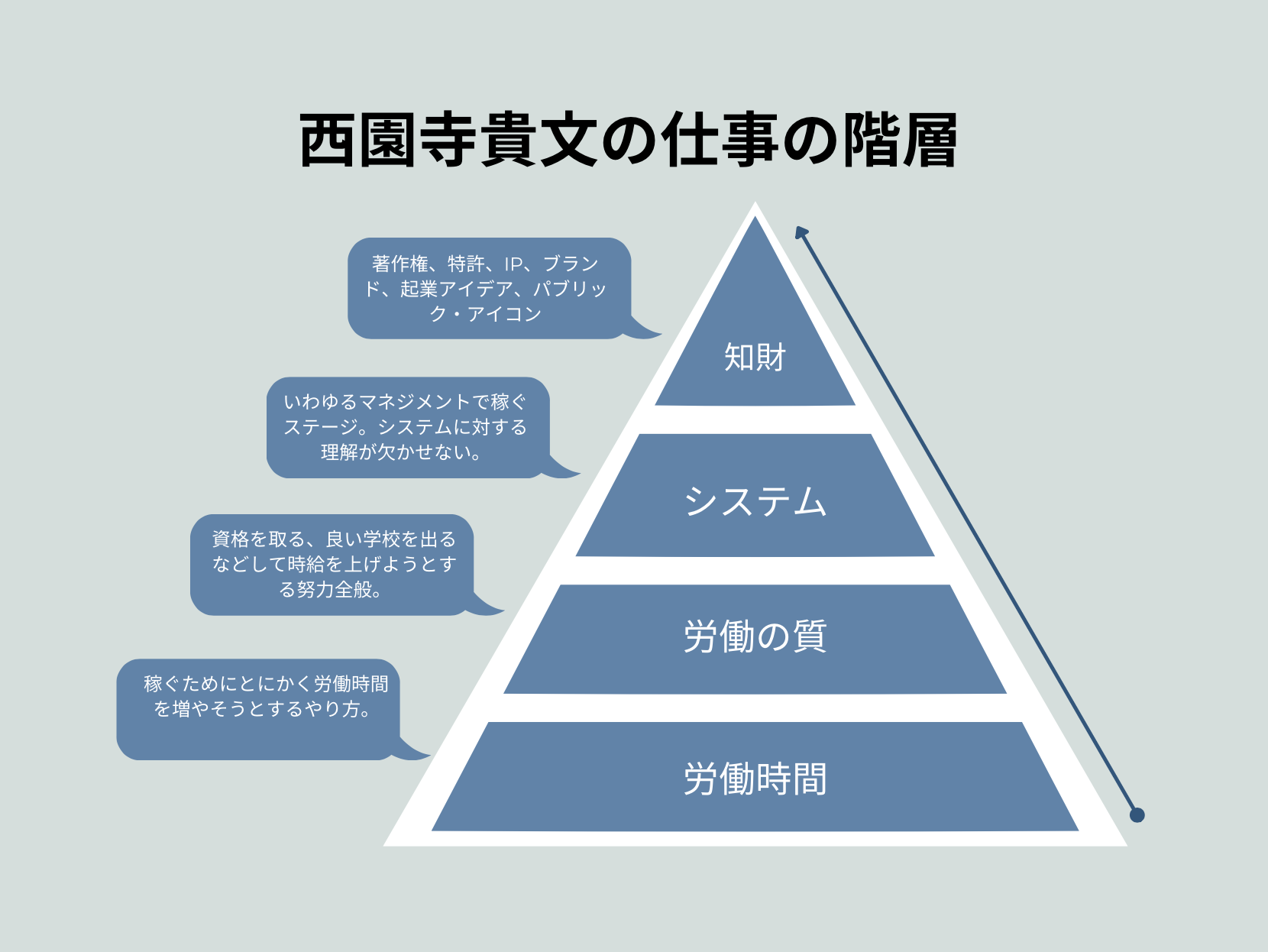
フロントエンド・バックエンドの本質でも触れましたが、

直列か並列か

というのは「システム」に対する深淵な問いです。

労働時間を増やして稼ぐ、資格をとって時給を上げる、みたいな発想から抜け出したい人はシステムに対する理解を深める必要があります。

（　時給と富裕層の秘密と本質　）

私のように20代で年収1000万円以上になりたいのなら、早くシステム以上の世界に来なさい、公認会計士資格とか司法試験とかやってても時間の無駄です。

「システムとは何か？」を数学的に理解しましょう。

システムとは要素のつながり、体系です。

そして、数学的に、

直列関係は掛け算
並列関係は足し算

となります。

数式を立案する際、関係する要素を網羅したら、その関係性を考えるのですが、まず関係性について

「直列的か？並列的か？」

と考えてみましょう。

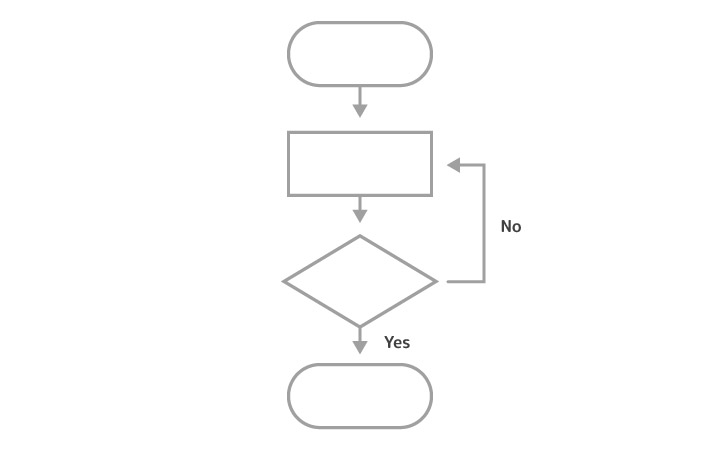
プログラマー、ゲームデザイナー、そのほかエンジニアリング関係の人はフローチャートを意識して生きていると思います。数理モデリングの際にも、このフローチャート的な発想は生きるかもしれません。

また、ABC予想じみた話になりますが、

足し算は掛け算より（構造的に）難しい

のです。

例えば12という数字を分解すると、

3×2×2＝12

で分解できます。

というのは、

6×2　＝ 12
3×4　＝ 12

も分解していくと一緒なのです。6が「3×2」で、4が「2×2」ですからね。

一方で、

1+1+1+…＝12
2+2+2+…＝12
7+5＝12

というように組み合わせがいくらでも出てきます。

また、四則演算についての基本的な理解については、「　問題解決の本質　」をお薦めします。

割り算とルートがいっちゃん難しい

数学・数式立案の基本ですが、

「割り算とルート」

がいっちゃん難しいです。

特に割り算は本当に奥が深い世界で、そのために「　LUXEM DNA　」の第1章のタイトルを「➗」にしたくらいです。

そもそも数の発展の体系と歴史から考えて、

割り算できない数がある

ということをピタゴラスちゃんが見つけてしまってからが大変だったのですが（割れない数を見つけた奴を殺した）、そこから無理数というものが生まれました。

√

とかですね。ルートです。

数式において分数や割り算が頻繁に現れるのは、さまざまな数学的な概念や関係性を表現するための重要な手段です。分数や割り算が持つ意味と役割についていくつか説明します。

比率と割合の表現: 分数は、数量の比率や割合を表現するために使用されます。例えば、 $a / b$ の形の分数は、 $a$ と $b$ の比率を示し、一方の量が他方の量に対してどれだけの部分を占めているかを示すことができます。
分割と分配: 分数や割り算は、量を分割して複数の部分に分けたり、ある量を複数の項目に分配する際に使用されます。例えば、 $a / b$ の分数は、 $a$ を $b$ 個の等しい部分に分割したり、 $a$ を $b$ と同じ数の項目に均等に分配することを意味します。
小数の表現: 小数は、分数の特殊なケースとみなすこともできます。例えば、小数 0.5 は分数 $1/2$ と等価です。数式において小数を分数で表現することで、計算や解析が容易になる場合があります。
分数の操作: 分数は代数的な操作を行う際に非常に便利です。分数同士の加算、減算、乗算、除算などの操作は、実世界の問題や数学的な問題を解く際に頻繁に行われます。
連続的な変化のモデリング: 割り算や分数は、連続的な変化をモデリングする際に使用されます。例えば、速度や密度の変化率を表現するために割り算が使われることがあります。

数式内での分数や割り算の出現は、数学的な関係や変換を的確に表現するための重要な手段であり、数学のさまざまな分野で広く使用されます。

ところで、ゼロの割り算がどうしてダメなのかちゃんとわかっていますか？

0の割り算が問題となるのは、割る数（除数）が0の場合に数学的な定義が成り立たないためです。0で割る操作は数学的に定義されておらず、このような操作を行うことは意味がなく、不適切な結果をもたらす可能性があります。以下にその理由を説明します。

定義の問題: 割り算は、数 $a$ を数 $b$ で割った結果を求める操作です。しかし、 $b$ が0の場合、 $a / b$ の結果をどのように定義するかが問題となります。0で割るという操作自体が数学的には不明確であり、意味を持たないため、割り算の定義が成り立ちません。
無限大や未定義の概念: 数 $a$ を0で割ると考えると、どのような数を割っても0になることになります。これは数学的に無限大や未定義の概念と関連しており、正確な結果を導くことができません。
数学的に不適切な結果: 0で割る操作が許可されると、数式や方程式内で不適切な計算が行われる可能性があります。これは数学的な論理や体系を乱し、正しい結果を得ることを阻害します。

したがって、数学的には0で割る操作は避けるべきです。プログラミングなどのコンピュータ科学分野でも、0で割ることはエラーや不正な動作を引き起こす原因となるため、注意が必要です。

東京大学などに受かった人は同値変形で「0」が重要なのはわかるはず

難関国公立などに受かった人は、分数を扱う際に、同値変形において「０」を基準にすること、０を基準点にして比較することの重要性を知っているはずです。

これは、「　構造的理解の本質　」の中でも触れたのですが、尺度の観点と結びつきます。

比例尺度には絶対的な0点があります。

間隔尺度（Interval Scale）と比例尺度（Ratio Scale）は、統計学や測定の文脈で使用される2つの尺度です。これらの尺度は数値データの特性を表現し、解釈するために用いられます。以下に、間隔尺度と比例尺度の違いを説明します。

間隔尺度（Interval Scale）:

間隔尺度は、数値データの特性を表現するための尺度で、順序関係や等間隔性を持ちますが、絶対的なゼロ点が存在しない特徴を持ちます。具体的な特性としては、以下のような点が挙げられます：

順序関係（Ordinality）: データの値は大小関係があります。すなわち、ある値が別の値よりも大きいか小さいかを比較することができます。
等間隔性（Equidistance）: データの間隔（差）には意味があります。間隔の差が同じだけの意味を持ちますが、絶対的なゼロ点が存在しないため、比率を計算することはできません。
絶対的なゼロ点の欠如（Absence of Absolute Zero）: 尺度の原点が固定されておらず、数値のゼロは任意的な位置です。例えば、温度尺度での摂氏0度や華氏0度は絶対的なゼロ点ではありません。

比例尺度（Ratio Scale）:

比例尺度は、数値データの特性を表現するための尺度で、順序関係や等間隔性だけでなく、絶対的なゼロ点も存在します。具体的な特性としては、以下のような点が挙げられます：

順序関係（Ordinality）: 間隔尺度と同様に、データの値は大小関係があります。
等間隔性（Equidistance）: 間隔尺度と同様に、データの間隔には意味があります。
絶対的なゼロ点の存在（Presence of Absolute Zero）: 尺度の原点が固定されており、数値のゼロは絶対的な位置です。例えば、身長や重さなどの物理的な尺度が比例尺度です。

比例尺度は、比率の計算や割合の評価が可能なため、より多くの情報を提供します。間隔尺度と比例尺度は、データの性質に応じて適切な尺度を選択する際に考慮すべき要素です。

つまり、割り算が数式に出てくるというのは、

「基準点」

が意識されているということです。

対比の概念もその延長にあります。

カウンティング・センスが必要

「文理の交差点」で触れましたが、基本的な数のセンス、数を数えるカウンティングセンスがないと、数式の立案はできません。

（「文理の交差点」本編より抜粋）

ですから、「数え方」というものをまず理解しないと、数式を考案できるようにはなりません。

割り算から始まる確率論

分数は可能性を表現するには好都合です。

可能性というのは全体に占める比例のことであり、全体に占める分量割合、そういったものです。だから分割と比例とを同時に表現する分数こそ、適任なのです。

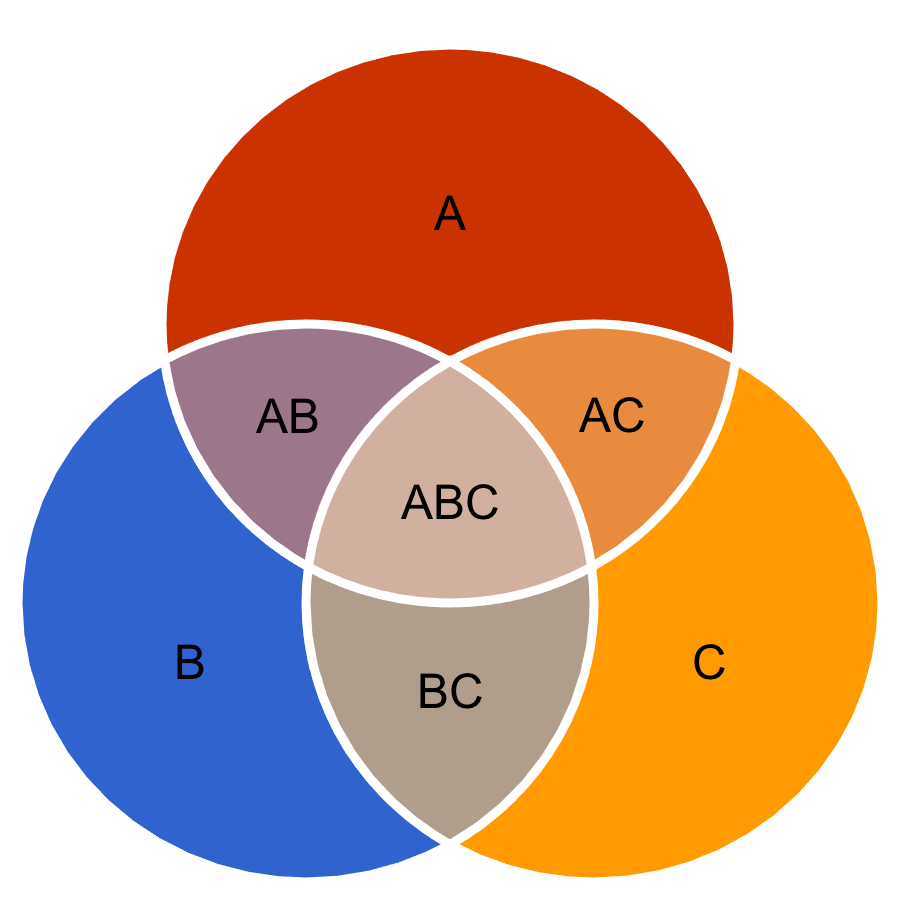
そして、確率論を論ずる上では、ベン図を理解する必要があります。

これは測度論とも関係してきますが、

という事象があった場合、ABCが同時に起こる場合やABCのどれかが起こる場合、AとBが同時に起こる場合やABのどれかが起こる場合、、、、、というものをしっかり分けて数えないといけないのです。

例えば、

A　＝　安い店　1/4
B　＝　美味い店　1/5
C　＝　早い店　1/3

だった場合に、

「高くて不味くて遅い店」

の確率を求める場合、

「安くて美味くて早い店」

の確率を全体（1=100%）から引く、という失敗をしてしまう。

以上の３つの丸のどことも重なっていない領域が「高くて不味くて遅い店」ですが、それを求める際に全体（1=100%）から「ABC」を引くだけではダメです。AB、AC、BC、、、などの他の領域もありますから。

https://gendai.media/articles/-/86674?page=3

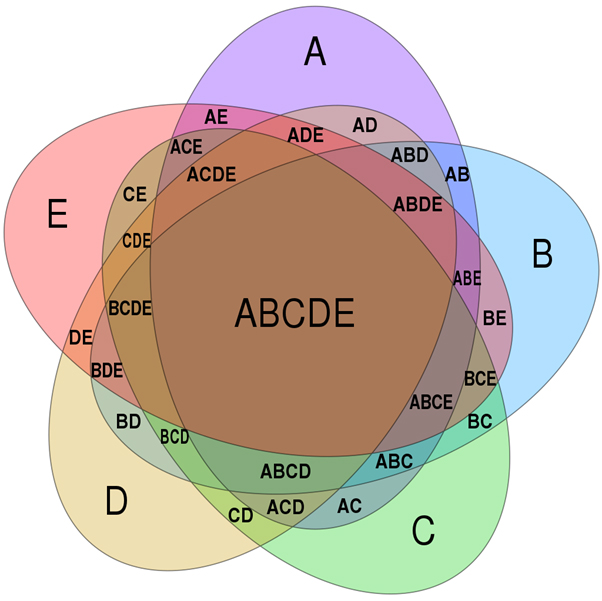
これがさらに複数になると余計に厄介。

「全体」を定義した上で、その全体の中で、どういう領域の割り当てがあるか、という感覚です。

全体をしっかりと定義して、その中の割り当てをしっかり数えられるようにならないと確率計算はできないのです。

統計学でおさえておくべき分布

個人的に、統計学でおさえておくべき分布は、

正規分布
対数正規分布
べき分布
幾何分布
指数分布
ポアソン分布
負の二項分布
ガンマ分布

だと思います。

もちろん正規分布が大事なのは言うまでもありませんが、

正規分布の数式を今書いて

と言われたら大まかにでも書き出すことができますか？

なぜ書けないのかというと、

原型が

e^-x

であることを理解していないからです。そして、これを理解すると、グッと深い世界に入ることができます。

確率計算＝積分計算をするときの目処がつくからです。

「偏差値55って上位何%だっけ」

という時に、ある程度わかるようになる。

次に大事なのがポアソン分布です。

一定期間で平均でλ回起こる現象が、k回起こる確率、というものです。

ポアソン分布はλとkの二つのパラメーターだけですが、分母に「階乗」があることに注目しましょう。階乗は最強の関数です。これが「k=回数」の階乗、ということは「多い回数の出来事」がほぼ起こらないようになる数式だということです。

階乗やガンマ関数は、一般的な自然現象と直接的な対応は持ちませんが、数学的な概念として広く応用されています。階乗は非常に急速に増加する関数であり、その特性はさまざまな現象や数学的モデルの解析に利用されています。一方、ガンマ関数は階乗を一般化した関数であり、その性質は統計学や数理物理学、工学などの分野で応用されています。以下に具体的な例を挙げてみましょう。

階乗の応用:

コンビネーションと組み合わせ論: 階乗は、組み合わせ論や確率論の分野で、要素の選び方や順序に関する計算に使用されます。物事の順序や組み合わせを考慮する場合に重要な役割を果たします。
数列と漸化式: 階乗は、数列や漸化式の解析にも利用されます。階乗を含む数列や漸化式は、自然現象のモデリングや数学的な興味の対象となることがあります。

ガンマ関数の応用:

統計学: ガンマ関数は、確率分布の形状パラメータや尤度関数の正規化に関連して使用されます。統計モデルの構築やデータの分析において重要です。
物理学: ガンマ関数は、量子力学や統計力学、場の理論などの物理学の分野で現れることがあります。統計力学の分野では、粒子の分布やエネルギー準位の計算に関与します。
工学: ガンマ関数は、信号処理や制御工学、通信工学などで応用されます。特に、信号の周波数領域の解析やシステムの特性評価に関連します。

階乗やガンマ関数は、自然界の特定の現象とは直接的な対応を持たないものの、数学的な道具として広く応用されています。これらの関数は、さまざまな分野で問題のモデリングや解析に使用され、その性質や特徴が応用範囲を広げる上で重要な役割を果たしています。

データと推計

パーソルが中央大教授と共に出した将来の労働市場に関する推計が参考になります。

https://rc.persol-group.co.jp/thinktank/spe/roudou2030/files/future_population_2030_4.pdf

データを集めてきて、それらを組み合わせてデータを生成して、そこから予測をしているというプロセスが見えます。

今回の「予測モデル」は、「労働需要ブロック」「労働供給ブロック」「需給調整ブロック」の3ブロックからなり、相互に作用するこの3つのブロックを用いてシミュレーションを繰り返すことで、より精緻な予測を目指しました。「労働需要ブロック」では、2030年の産業計の労働需要を算出。「労働供給ブロック」では、2030年の労働力人口を算出。3つ目の「需給調整ブロック」では、「市場が埋めようとする需要と供給の差」を調整しました。労働需要量と労働供給量を用いてマッチングを行い、就業者数と失業者数を推計。その失業者数から実質賃金を推計し、その賃金レートにおける需給量を再び推計し、結果を得ました。

https://rc.persol-group.co.jp/thinktank/spe/roudou2030/

天気予報の的中率から考えるデータ粒度

データの粒度とは？

データの粒度とは、データがどれだけ細かく観測・収集されているかを指す概念です。粒度が細かいほど、データが詳細かつ微細なレベルで得られています。逆に、粒度が荒いと、データは大まかな情報しか含まないことがあります。

例えば、気象データにおいて、データの粒度が高い場合、短い時間間隔で気温、湿度、風速などの情報が得られます。これに対して、データの粒度が低い場合、一日ごとの平均的な気象情報が得られるかもしれません。データ粒度は、データ収集の頻度や観測点の密度によって決まります。

数学的予測モデルとは？

数学的予測モデルとは、数学的な方程式やアルゴリズムを用いて、未来の出来事や現象を予測するためのモデルです。例えば、気象予報においては、過去の気象データを元にして気象現象の動きや変化をモデル化し、未来の天気を予測します。

予測モデルは、複雑な関係やパターンを理解し、未来のデータポイントを生成するために利用されます。これには統計学や数値解析、機械学習、シミュレーションなどの手法が用いられます。モデルの選択やパラメータ調整によって、予測の精度や的中率が変わることがあります。

データの粒度と数学的予測モデルの関係

データの粒度と数学的予測モデルは、互いに密接な関係があります。データの粒度が高ければ、細かい変動やパターンをモデルに取り入れることができますが、その分データ収集と処理にかかるコストが増えます。逆に、データの粒度が低い場合、モデルは大まかな傾向しか捉えられませんが、計算コストは低く抑えられます。

適切なデータの粒度を選択することは、予測モデルの性能に大きな影響を与えます。粒度が細かすぎると、モデルがノイズを捉える可能性があります。一方、粒度が低すぎると、モデルが現実の変動や特徴を十分に捉えられないかもしれません。

予測モデルの開発においては、データの粒度と予測精度のバランスを見極める必要があります。このバランスを適切に保つことで、効果的な予測が実現されます。

天気予報の的中率とは？

気象予報は、私たちの日常生活やビジネス活動に大きな影響を及ぼす重要な要素です。ウェザーニュースなどの天気予報サービスが提供する予報は、近年の技術革新により非常に高い的中率を誇ることがあります。これにはいくつかの要因が絡んでいますが、その中でもデータ粒度の適切な利用が大きな鍵となっています。

データの収集と分析

天気予報の的中率向上には、膨大な気象データを収集し、高度な数学的モデルに基づいて分析するプロセスが関与します。気象データは、気温、湿度、風速、気圧、雲の量などのパラメータから成り立ちます。これらのデータを多数の観測点から収集し、リアルタイムで更新されることで、精緻な予測が可能となります。

数学的モデルの構築と学習

天気予報においては、複雑な気象現象を表すために、数学的なモデルが用いられます。これには気象学の知識や数値計算が結集され、大気の動きや変化を模倣する仕組みが組み込まれます。また、機械学習アルゴリズムを用いて、過去の気象データと実際の天候の関係を学習することで、より精確な予測が可能となります。

データ粒度の重要性

データの粒度とは、データがどれだけ細かく観測されているかを指します。データ粒度が細かいほど、より詳細な情報を得ることができますが、同時に処理コストも高まります。データ粒度の適切なバランスを見つけることが的中率向上に欠かせないポイントです。

数学的予測におけるデータ粒度の役割

データ粒度は、数学的予測の正確性に大きな影響を与えます。例えば、気象データの観測地点をより多く配置することで、地域ごとの微細な気象変化を正確に予測することができます。これに対し、データ粒度が低い場合、広範な領域の平均的な予測しか行えない可能性があります。一方で、データ粒度を細かくしすぎると、計算コストが高まることや、計算の過程での誤差が増える可能性もあります。適切なデータ粒度を選択することで、的中率を高めながら、効率的な予測モデルを構築することが求められます。

まとめ

天気予報の的中率向上には、豊富な気象データと数学的モデルの組み合わせが欠かせません。その中で、データ粒度の選択は的中率向上の鍵となります。適切なバランスを見つけつつ、高度な計算技術とデータ解析により、私たちの日々の生活を支える正確な天気予報が提供されています。

離散と連続の架け橋

人生アドベンチャー「離散」、人生アドベンチャー「連続」も参照してください

離散的なものを連続に、または連続的なものを離散に変換するためには、数学的な技術や手法がいくつか存在します。以下に、そのいくつかの例を挙げてみましょう。

離散のものを連続に変換する技術:

補間 (Interpolation):
- 線形補間
- ラグランジュ補間
- スプライン補間
フーリエ変換 (Fourier Transform):
- 離散フーリエ変換 (DFT)
- 高速フーリエ変換 (FFT)
- 非等間隔フーリエ変換
ウェーブレット変換 (Wavelet Transform):
- 離散ウェーブレット変換 (DWT)
- 近似ウェーブレット変換 (AWT)
- 連続ウェーブレット変換 (CWT)
カーネル密度推定 (Kernel Density Estimation):
- パラゴン法
- グレースン法
- シルバーマン法

連続のものを離散に変換する技術:

離散化 (Discretization):
- 空間の離散化
- 時間の離散化
- 数値グリッドの生成
サンプリング (Sampling):
- ナイキスト・シャノンサンプリング定理
- アンダーサンプリング
- オーバーサンプリング
数値積分 (Numerical Integration):
- 台形則
- シンプソン則
- 数値積分法の一般化
有限要素法 (Finite Element Method):
- 領域の分割
- 有限要素の定義
- 境界条件の適用
数値微分 (Numerical Differentiation):
- 中心差分法
- 前進差分法
- 後退差分法
サンプリング定理 (Sampling Theorem):
- ナイキスト周波数
- 高周波成分のエイリアシング
- 離散サンプリングの定理
モンテカルロ法 (Monte Carlo Method):
- ランダムサンプリング
- モンテカルロ積分
- 確率分布のシミュレーション

これらの技術は、数学的モデリングや数値解析において、離散と連続の間でデータや問題を変換するために重要な役割を果たしています。

離散的なものを連続に変換する方法:

補間 (Interpolation):
- 離散的なデータポイントを連続的な関数で近似するための手法です。ラグランジュ補間やスプライン補間などが一般的な方法です。
フーリエ変換 (Fourier Transform):
- 離散的なデータ列を周波数ドメインに変換する方法で、連続的な波形を解析する際に利用されます。
ウェーブレット変換 (Wavelet Transform):
- 高い時間または空間解像度を持つ一連の関数（ウェーブレット）を用いて、離散データを連続的な領域に変換します。

ラグランジュ補間:

ラグランジュ補間は、与えられたデータポイント（x, yの組み合わせ）を通過する多項式を求める方法です。データポイントが n+1 個ある場合、n 次の多項式を用いてデータポイントを完全に通過するように近似します。この多項式は次のように表されます。

P(x) = y₀ * L₀(x) + y₁ * L₁(x) + … + yₙ * Lₙ(x)

ここで、Lᵢ(x) はラグランジュ基底関数で、それぞれのデータポイントに関連するものです。ラグランジュ基底関数はデータポイントを通過する性質を持ち、与えられたデータに対して滑らかな曲線を生成します。

スプライン補間:

スプライン補間は、データポイントを通過するなめらかな曲線を生成するための方法で、特にデータ間の曲率や滑らかさを考慮した補間法です。スプライン補間は、通常、区間ごとに異なる多項式（スプライン関数）を使用してデータを近似します。

スプライン補間の一般的な手順は次のとおりです。

データポイントを区間に分割し、それぞれの区間でのスプライン関数を決定します。
各区間でのスプライン関数は、データポイントを通過し、区間の境界点での連続性や滑らかさを保つように設計されます。
スプライン関数がすべての区間で連続かつ滑らかであるため、データ全体でなめらかな補間曲線が得られます。

スプライン補間は、ラグランジュ補間よりもデータ間の曲率を考慮した精緻な補間を行うことができるため、より複雑なデータセットに適しています。

どちらの方法もデータの補間に使われるため、具体的なデータや用途に応じて適切な方法を選ぶことが重要です。

連続的なものを離散に変換する方法:

離散化 (Discretization):
- 連続的な領域を有限な区間やステップに分割することで、連続的な問題を離散的な問題に変換します。微分方程式を差分方程式に変換する際に使われます。
サンプリング (Sampling):
- 連続的な信号や波形を離散的なデータポイントに変換する方法です。アナログ信号をデジタル信号に変換する際に使われます。
ディジタルフィルタリング (Digital Filtering):
- 連続的な信号をディジタルフィルタを用いて離散的な信号に変換する方法です。信号処理や通信技術で使用されます。
数値積分 (Numerical Integration):
- 連続的な関数を離散的なデータに変換するための数値的な手法です。台形則やシンプソン則などが使用されます。

これらの技術や手法は、数学や科学のさまざまな分野で広く活用されており、実世界の問題を解析する際に非常に重要です。

差分法

差分法（Difference Method）と差分方程式（Difference Equation）は、数値計算や数理モデリングにおいて使われる重要な手法です。これらは微分方程式や差分演算子を用いて、連続的な問題を離散的な形式で近似・解析するために利用されます。

差分法 (Difference Method):

差分法は、連続的な問題を有限なステップや間隔（差分）に分割し、それぞれのステップでの値を計算する方法です。主に微分方程式や偏微分方程式などを離散的に近似する際に使用されます。差分法の一般的な手順は以下の通りです：

問題の連続的な領域を有限なステップに分割（離散化）します。
差分方程式や差分演算子を用いて、各ステップでの値の更新式を導出します。
初期条件や境界条件を設定し、初期値を与えます。
時間や空間のステップを進めながら、計算を実行して連続的な問題を離散的に近似します。

差分方程式 (Difference Equation):

差分方程式は、連続的な時間や空間における微分方程式を離散的な形式で表現したものです。差分方程式は、逐次的に計算されるステップごとの値を求めるために使われます。一般的に、現在の時刻や位置の値を未来の時刻や位置の値と関連付ける関係を記述します。

ビッグデータが世界を変えた

ビッグデータ（Big Data）とは、非常に大規模で複雑なデータセットを指す用語です。これらのデータは、通常のデータベース管理システムやデータ処理ツールでは処理が難しいほどに大量で、高速なデータ収集、保存、分析が必要です。ビッグデータは、インターネット、センサーネットワーク、ソーシャルメディア、経済取引などから生成されるさまざまな情報源から集められます。

ビッグデータの特徴:

ボリューム（Volume）: ビッグデータは、通常のデータベース管理システムやツールでは扱いきれないほど膨大な量のデータを指します。この大量のデータは、テキスト、画像、音声、ビデオなど、さまざまな形式で存在することがあります。
多様性（Variety）: ビッグデータは、異なる種類や形式のデータが混在していることがあります。構造化データ（テーブル形式のデータ）、半構造化データ（XMLやJSONなどの形式）、非構造化データ（テキスト、画像、動画など）が含まれます。
速度（Velocity）: ビッグデータは高速で生成されることがあり、リアルタイムまたは近似リアルタイムで処理する必要があります。例えば、センサーデータやソーシャルメディアの投稿などがこれに該当します。
正確さ（Veracity）: ビッグデータは、品質や信頼性に関する問題を抱えることがあります。データの信頼性や正確さを確保するための手段が必要です。
価値（Value）: ビッグデータは、適切な分析と処理を行うことで、新たな洞察や価値をもたらす可能性があります。例えば、顧客の嗜好を理解して個別にターゲットするマーケティング戦略を策定するなど。

ビッグデータを活用するためには、適切なデータ収集、ストレージ、処理、分析のインフラやツールが必要です。これには、分散処理フレームワーク（例：Hadoop）、クラウドコンピューティング、データベース技術、機械学習、人工知能などが含まれます。ビッグデータの活用により、新たなビジネス戦略の発見、効率の向上、リスクの管理、科学的な研究の進展などが可能になります。

マーケターという職業は実は2013年に終わっていて、それまでに地位を築いた人の勝ち逃げゲームになっている。

＝＝＝

＠西園寺貴文（憧れはゴルゴ13）#+6σの男

"make you feel, make you think."

SGT&BD
(Saionji General Trading & Business Development)

新たなるハイクラスエリート層はここから生まれる

Lose Yourself , Change Yourself.（変えることのできるものについて、それを変えるだけの勇気を我らに与えたまえ。変えることのできないものについては、それを受け入れられる冷静さを与えたまえ。そして、変えることのできるものと、変えることのできないものとを、見分ける知恵を与えたまえ。）

説明しよう！西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である！平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである！「働かざること山の如し」。彼がただのニートと違う点はたった１つだけ！そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。