「三角関数より金融経済」の議員氏のサイトを覗くと、経済学部在籍時代を振り返り「旅とテニスに明け暮れた日々。机の上では学ぶことのできない、多くを学びました」とあり、机の上での学びの重要性、机の上での学びを軽んじた行く末をこうして身をもって体現しているのだと感嘆した。
— 松崎貴之 (@gelcyz) May 18, 2022
「三角関数より金融経済」って学問へのsin刻な冒涜だよ。理系への当てcosりなのかな。tan絡的な思考だと思うわ。
— リアル世界観 (@real_do_estate) May 19, 2022
【文系が語る】
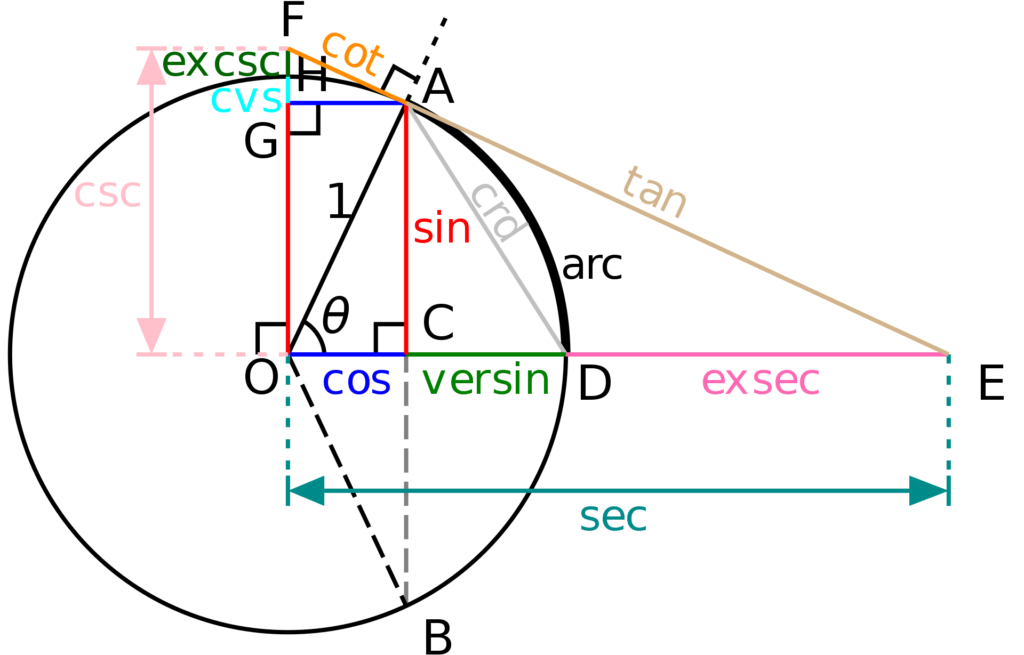
三角関数は、円関数であり、三角という幾何の基礎と、円という幾何の基礎を接続させるのであります。
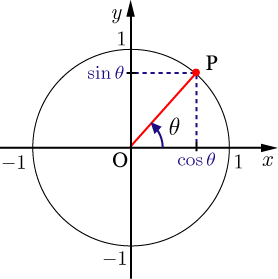
https://w3e.kanazawa-it.ac.jp/math/ ←就職率トップで有名な金沢工業大学のコンテンツすごい
すなわち、円の中心点から、x軸、y軸を考えました時、円の内部で中心点と円周に頂点が内接、x軸に辺が重なる直角三角形を成立させることができこの三角形の斜辺が円の半径となりますが、
円とは中心点から同じ距離の点の集合であるため、これを関数化=定式化いたしますと
X^2+y^2=1
といいますように、斜辺=円の半径をかの有名なピタゴラスの定理(三平方の定理)によって定式化することができるのでございます。
正直、幾何で一番大事なのはピタゴラスの定理でございます
https://www.programming-edu.com/2017/06/01/read-figures/
https://jp.quora.com/pitagorasu-no-teiri-no-kantan-na-shoumei-houhou-arima-suka
すなわち、円とは、xとyの合計が常に一定の、関数として定式化できるのであります。
さらに、斜辺=円の半径の一定性のかたわらで、x(底辺)とy(高さ)を可変させることができるのですが、それを動的にした時に円の中心点でみる三角の角度も変化していくことになります
そしてその可変の様子は、
x(底辺)部分が縮めばy(高さ)部分が伸び、縦に細長い三角形、究極は縦線に、
y(高さ)部分が縮めばx(底辺)部分が伸び、横に細長い三角形、究極は横線になり、
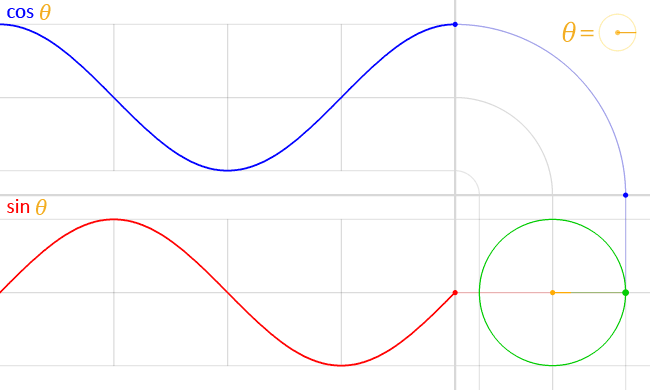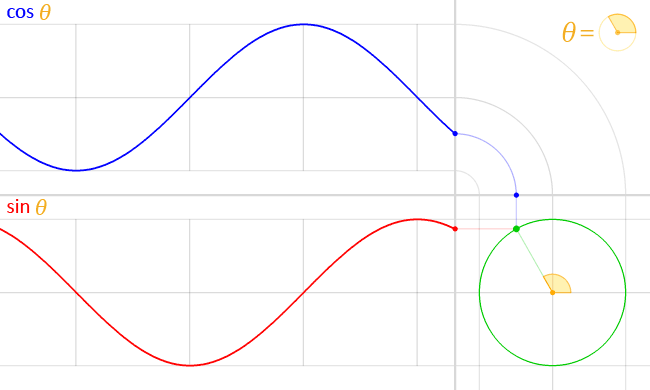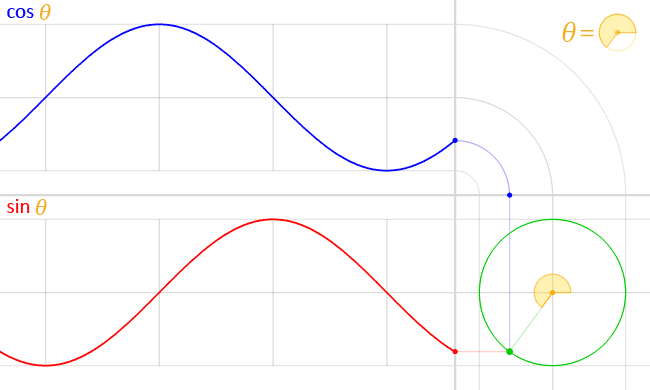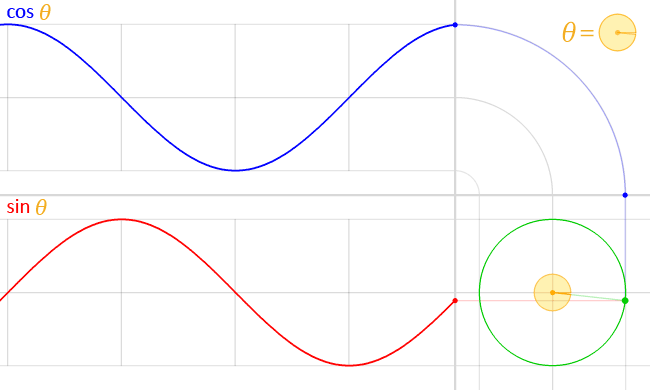
xとyの数値の増え方、減り方を別で図示するとちょうど重ならない波線になります
ここで、波線とも接続するわけです
https://ja.m.wikipedia.org/wiki/ファイル:Circle_cos_sin.gif
三角関数はある角度における辺と辺の比ですが、
上記のように円の中で内接した直角三角形で考えますと、
角度が鋭角すなわち横に細長く横線(y=高さがなく、x=底辺が長い)に近づいてるとき、
角度が直角すなわち縦に長く縦線に近づいているとき、
それぞれにおける
xとyの比
という考え方もでき、
斜辺=円の半径=常に一定に対するyの比を見るのが俗に言うサイン、xの比を見るのがコサインでございます
タンジェントはxに対するyの比すなわち底辺に対する高さでございます
https://ja.m.wikipedia.org/wiki/三角関数
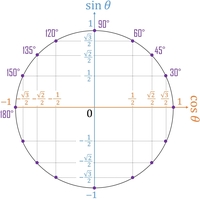



サインもコサインも、
究極的に『縦線』『横線』になることを考えると斜辺に対する比はMAXでは斜辺と同化、同じ、すなわち1:1でしかありません
ところがタンジェントは、底辺に対して高さが数倍、あるいはその逆になることがあります
しかもxが縮みながらyが伸びてくので異様な比になっていきます
常に一定である斜辺に対して最大値が斜辺と同化であるサイン、コサインに対して、
タンジェントはそもそもの定義として斜辺ではございません
https://www.google.co.jp/amp/s/www.nli-research.co.jp/report/detail/id=67789%3fmobileapp=1&site=nli
このように、
- 三角形
- 円
- 波線
を繋いでいるのが三角関数であり、
三角関数はやがてフーリエ変換と接続するととんでもない世界になってきます
何がサーキュレーションしているのか、しているとしてその構造は?を分析するのはマーケティングにも役立ちます
また、
より一層、
#
三角関数
三角関数公式
三角関数金融
三角関数とは
三角関数わかりやすく
三角関数表
三角関数の合成
三角関数より金融経済
三角関数何に使う
三角関数計算
三角関数公式集
三角関数公式 覚え方
三角関数公式 tan
三角関数公式 証明
三角関数公式 合成
三角関数公式 和積
三角関数公式 積分
三角関数公式 二倍角
三角関数公式 角度の求め方
三角関数金融工学
三角関数金融教育
三角関数とは わかりやすく
三角関数とはなにか
三角関数表 作り方
三角関数表 求め方
三角関数表 計算
三角関数表 ラジアン
三角関数表 一覧
三角関数表示
三角関数表 使い方
三角関数表とは
三角関数表 マイナス
三角関数の合成 cos
三角関数の合成 最大最小
三角関数の合成 α
三角関数の合成 なぜ
三角関数の合成 公式
三角関数の合成 マイナス
三角関数の合成 範囲
三角関数の合成 わかりやすく
三角関数の合成 2θ
三角関数計算アプリ
三角関数計算ツール
三角関数計算サイト
三角関数計算機
三角関数計算方法
三角関数計算問題
三角関数計算ソフト
三角関数計算 プログラム
三角関数グラフ
三角関数 辺の長さ
三角関数 辺の求め方
三角関数 アプリ
三角関数 暗記
三角関数 辺
三角関数 アーク
三角関数 arc
三角関数 アニメーション
三角関数 辺を求める
三角関数 アプリ iphone
三角関数いらない
三角関数いつ習う
三角関数 一覧
三角関数いらない議員
三角関数 位相
三角関数 いつ
三角関数 一般角
三角関数 意味
三角関数 位相 公式
三角関数 一般解
三角関数 wiki
三角関数 裏ワザ
三角関数 美しい
三角関数 unity
三角関数 宇宙
三角関数 英語
三角関数 円
三角関数 エクセル
三角関数 円グラフ
三角関数 円 座標
三角関数 鋭角
三角関数 e
三角関数 演習
三角関数 英語 略
三角関数 円の面積
三角関数 覚え方
三角関数 応用
三角関数 応用問題
三角関数 覚えること
三角関数 置き換え
三角関数 面白い問題
三角関数 面白いグラフ
三角関数 オイラー
三角関数 面白い
三角関数 教え方
三角関数 加法定理
三角関数 角度の求め方
三角関数 和積
三角関数 角度
三角関数 関係式
三角関数 加法定理 証明
三角関数 解の個数
三角関数 加法定理 覚え方
三角関数 掛け算
三角関数 回転
三角関数 極限
三角関数 近似
三角関数 基礎
三角関数 基本
三角関数 極限 はさみうち
三角関数 虚数
三角関数 極限 証明
三角関数 基本公式
三角関数 距離
三角関数 極限 例題
三角関数 区分求積法
三角関数 空間図形
三角関数 クイズ
三角関数 くくる
三角関数 くるくる
三角関数 詳しく
三角関数 クレーン
三角関数 くもん
三角関数 組み合わせ
三角関数 クリア
三角関数 計算
三角関数 計算機
三角関数 計算方法
三角関数 計算 公式
三角関数 計算 エクセル
三角関数 建築
三角関数 計算問題
三角関数 計算 ラジアン
三角関数 計算の仕方
三角関数 計算アプリ
三角関数 公式
三角関数 公式 覚え方
三角関数 公式集
三角関数 公式 tan
三角関数 弧度法
三角関数 高校
三角関数 公式 証明
三角関数 cot
三角関数 公式 覚え方 語呂合わせ
三角関数 cos
三角関数 最大最小
三角関数 三倍角
三角関数 サインコサインタンジェント
三角関数 三角比
三角関数 三角形の面積
三角関数 最大最小 難問
三角関数 参考書
三角関数 最大最小 わかりやすく
三角関数 最大最小 置き換え
三角関数 サイン
三角関数 周期
三角関数 象限
三角関数 θ 求め方
三角関数 sin
三角関数 証明
三角関数 θ
三角関数 式
三角関数 指数関数
三角関数 斜辺
三角関数 導関数
三角関数 数2
三角関数 数1
三角関数 数式
三角関数 漸化式
三角関数 数値
三角関数 数列
三角関数 数何
三角関数 数値計算
三角関数 数三
三角関数 数列 極限
三角関数 積分
三角関数 積和
三角関数 性質
三角関数 sec
三角関数 積分 公式
三角関数 積分 大学
三角関数 正弦定理
三角関数 積分 置換
三角関数 積分 例題
三角関数 正負
三角関数 相互関係
三角関数 測量
三角関数 相互関係 問題
三角関数 双曲線関数
三角関数 相似
三角関数 相互関係 証明
三角関数 そもそも
三角関数 相互関係 tan
三角関数 測量 問題
三角関数 速度
三角関数 tan
三角関数 単位円
三角関数 足し算
三角関数 tan グラフ
三角関数 高さを求める
三角関数 単位円 解き方
三角関数 tan 公式
三角関数 対称式
三角関数 単位円 なぜ
三角関数 足し算 公式
三角関数 中学
三角関数 値
三角関数 置換積分
三角関数 直交性
三角関数 直角三角形
三角関数 長さ
三角関数 値 求め方
三角関数 置換
三角関数 直角三角形以外
三角関数 中3
三角関数 使い道
三角関数 ツール
三角関数 使われているところ
三角関数 使わない
三角関数 使い分け
三角関数 使われているもの
三角関数 使う仕事
三角関数 使い方 図面
三角関数 弦の長さ
三角関数 使える条件
三角関数 定義
三角関数 定理
三角関数 定積分
三角関数 テイラー展開
三角関数 点の回転
三角関数 展開
三角関数 定積分 例題
三角関数 底辺
三角関数 底辺 高さ
三角関数 底辺 角度
三角関数 twitter
三角関数 解き方
三角関数 等式
三角関数 トライ
三角関数 東大
三角関数 とある男
三角関数 等式の証明 コツ
三角関数 等式 証明
三角関数 統計
三角関数なくなる
三角関数なん j
三角関数 何に使う
三角関数 何年生
三角関数 なす角
三角関数 習う時期
三角関数 内接円
三角関数 長さ 計算
三角関数 内積
三角関数 何を求めている
三角関数 二倍角
三角関数 二乗
三角関数 日常生活
三角関数 入試問題
三角関数 二等辺三角形
三角関数 二乗 積分
三角関数 二直線のなす角
三角関数 二次関数
三角関数 入門
三角関数 二次方程式
三角関数 numpy
numbers 三角関数
三角関数 ネイピア数
三角関数 値を求める
三角関数 値 表
三角関数 値 覚え方
三角関数 値から角度
三角関数 値の範囲
三角関数 値を求めよ
三角関数 ネタ
三角関数 の性質
三角関数 ノート
三角関数 の相互関係
三角関数 の公式
三角関数 の応用
三角関数 のグラフ
三角関数 の最大最小
三角関数 の積分
三角関数 の極限
三角関数 半角の公式
三角関数 範囲
三角関数 波
三角関数 範囲 合成
三角関数 範囲指定
三角関数 早見表
三角関数 半径
三角関数 発見者
三角関数 波形
三角関数 半角 公式 覚え方
三角関数 表
三角関数 表 覚え方
三角関数 比
三角関数 筆記体
三角関数 比率
三角関数 引き算
三角関数 表 ラジアン
三角関数 非線形
三角関数 必要性
三角関数 引数
三角関数 不等式
三角関数 不等式 tan
三角関数 複素数
三角関数 不等式 応用
三角関数 フーリエ変換
三角関数 不等式 場合分け
三角関数 符号
三角関数 不定積分
三角関数 不等式 範囲 tan
三角関数 不等式 練習問題
三角関数 変換
三角関数 変形
三角関数 平行移動
三角関数 変換 コツ
三角関数 偏微分
三角関数 平方根
三角関数 平均値
三角関数 平均
三角関数 変域
三角関数 変形 コツ
三角関数 方程式
三角関数 方程式 計算
三角関数 方程式 単位円
三角関数 方程式 不等式
三角関数 本
三角関数 方程式 範囲
三角関数 本質
三角関数 法則
三角関数 方程式 tan
三角関数 方程式 応用
三角関数 まとめ
三角関数 マイナス
三角関数 マクローリン展開
三角関数 マクローリン
三角関数 マイナスπ
三角関数 マイナス1乗
三角関数 負の角度
三角関数 マスター
三角関数 まとめる
三角関数 マイナスの時
三角関数みずほ
三角関数 身の回り
三角関数 身近な例
三角関数 見つけた人
三角関数 見分け方
三角関数 身近
三角関数 満たすθの値
三角関数 難しい
三角関数 無限級数
三角関数 無限大
三角関数 無限積
三角関数 無限和
三角関数 無理数
三角関数 難しい問題
三角関数 無限
三角関数 無限積分
三角関数 難しすぎ
三角関数 面積
三角関数 面積の公式
三角関数 面積 積分
三角関数 面積 求め方
三角関数 面積計算
三角関数 面積 cos
三角関数 めんどくさい
三角関数 メリット
三角関数 問題
三角関数 求め方
三角関数 問題 pdf
三角関数 問題集
三角関数 問題 中学
三角関数 模試
三角関数 求める
三角関数 目的
三角関数 問題 解説
三角関数 文字式
三角関数 やり方
三角関数 役に立つ
三角関数 山の高さ
三角関数 役に立たない
三角関数 やばい
三角関数 やり直し
三角関数 やさしい
三角関数 役立つ
三角関数 約分
三角関数 有名角
三角関数 有理化
三角関数 有名角じゃない
三角関数 有名問題
三角関数 有理数
三角関数 有理関数 積分
三角関数 有名角 表
三角関数 有効数字
三角関数 ユーチューブ
三角関数 由来
三角関数よりも
三角関数よりも金融
三角関数 余弦定理
三角関数 余弦
三角関数 用途
三角関数 余角
三角関数 youtube
三角関数 四倍角
三角関数 用語
三角関数 ラジアン
三角関数 ラプラス変換
三角関数 ラジアンとは
三角関数 ラジアン 変換
三角関数 ラジアン 計算
三角関数 ラジアン 表
三角関数 ラジオ
三角関数 ラジアン 覚え方
三角関数 ラジアン マイナス
三角関数 ラジアン 問題
三角関数 理解できない
三角関数 領域
三角関数 利用
三角関数 力
三角関数 立体
三角関数 理系ラボ
三角関数 リミット
三角関数 理解
三角関数 力学
三角関数 理屈
三角関数 累乗 積分
三角関数 ルート
三角関数 累乗
三角関数 累乗 微分
三角関数 ルート 積分
三角関数 ルート3
三角関数 ルート2
三角関数 ルート 微分
三角関数 累乗 不定積分
三角関数 ルート5
三角関数 例題
三角関数 歴史
三角関数 連立方程式
三角関数 例
三角関数 例題集
三角関数 連続性 証明
三角関数 練習問題 pdf
三角関数 連続
三角関数 恋愛
三角関数 歴史 日本
三角関数 六角形
三角関数 ローラン展開
三角関数 論文
三角関数 ロボット
ロピタルの定理 三角関数
ログ 三角関数
ログの微分 三角関数
ロンスキー行列 三角関数
六分儀 三角関数
ros c++ 三角関数
三角関数 和の公式
三角関数 わせき
三角関数 和と積の公式
三角関数 わからない
三角関数 和と積の公式 覚え方
三角関数 割り算
三角関数 わせきせきわ
三角関数 和と積の公式 覚えるべき
三角関数 和石の公式
三角関数 を含む方程式
三角関数 を含む不等式
三角関数 を英語で
word 三角関数 グラフ
word 三角関数 二乗
word 三角関数
wolfram alpha 三角関数
word 三角関数 ショートカット
word 数式 三角関数
三角関数 n倍角
三角関数 n乗 積分
三角関数 n次導関数
三角関数 n乗 微分
三角関数 nπ
三角関数 nc旋盤
三角関数 nhk
三角関数 外接円
三角関数 学年
三角関数 概念
三角関数 学習
三角関数 学習指導要領
三角関数 概形
三角関数 ガウス
三角関数 画像処理
三角関数 学習指導案
三角関数 外接円 面積
三角関数 逆関数
三角関数 逆関数 微分
三角関数 逆関数 積分
三角関数 行列
三角関数 逆
三角関数 逆関数 求め方
三角関数 逆数 積分
三角関数 嫌い
三角関数 逆算
三角関数 逆関数 計算
三角関数 グラフ
三角関数 グラフ 平行移動
三角関数 グラフ サイト
三角関数 グラフ 周期
三角関数 グラフ tan
三角関数 グラフ 読み取り
三角関数 グラフ 応用
三角関数 グラフ 問題
三角関数 グラフ 目盛り
三角関数 グラフ y軸との交点
三角関数 ゲーム
三角関数 現象
三角関数 原理
三角関数 geogebra
三角関数 原始関数
三角関数 合成
三角関数 合成 公式
三角関数 合成 cos
三角関数 合成 最大最小
三角関数 合成 マイナス
三角関数 合成 sin同士
三角関数 合成 範囲
三角関数 合成 α
三角関数 合成 なぜ
三角関数 合成 α 範囲
三角関数 座標
三角関数 座標平面
三角関数 座標 問題
三角関数 座標から角度を求める
三角関数 座標 回転
三角関数 座標 距離
三角関数 実生活
三角関数 次数下げ
三角関数 自動計算
三角関数 重要
三角関数 受験の月
三角関数 乗法定理
三角関数 授業
三角関数 実数解
三角関数 実数
三角関数 重要公式
三角関数 図
三角関数 図解
三角関数 図面
三角関数 ずらす
三角関数 図の書き方
三角関数 図 円
三角関数 絶対値
三角関数 絶対値 積分
三角関数 絶対値 不等式
三角関数 漸近線 求め方
三角関数 絶対値 微分
三角関数 漸近線
三角関数 前提知識
三角関数 全単射
三角関数 絶対値 外し方
三角関数 増減表
三角関数 増減
三角関数 増減表 書き方
三角関数 増減表 正負
三角関数 増減表 単位円
三角関数 高さ
三角関数 大学
三角関数 大事なこと
三角関数 高一
三角関数 代表角
三角関数 大学入試
三角関数 大小比較
三角関数 代入
三角関数 高二
三角関数 誰が考えた
三角関数 diy
三角関数 図形
三角関数 図形への応用
三角関数 図形問題
三角関数 図形の応用
三角関数 図形と計量
三角関数 図形 面積
三角関数 合成 図形的意味
数学 三角関数 図形
図形と方程式 三角関数
図形と計量 三角関数 違い
三角関数 電卓
三角関数 電気
三角関数 電卓 使い方
三角関数 電験
三角関数 電卓 アプリ
三角関数 できない
三角関数 できること
三角関数 deg
三角関数 データサイエンス
三角関数 デザイン
三角関数 度数表
三角関数 鈍角
三角関数 度数法
三角関数 動画
三角関数 導出
三角関数 どこで使う
三角関数 度
三角関数 土木
三角関数 ドリル
三角関数 導入
三角関数 倍角
三角関数 媒介変数表示
三角関数 倍角の公式
三角関数 倍角 半角
三角関数 媒介変数表示 問題
三角関数 場合分け
三角関数 倍角 微分
三角関数 倍角の公式 証明
三角関数 倍角 公式 覚え方
三角関数 微分
三角関数 微分 公式
三角関数 微積
三角関数 微分 証明
三角関数 微分 例題
三角関数 微分 sin2x
三角関数 微分 やり方
三角関数 微分方程式
三角関数 微分 合成関数
三角関数 ビジネス
三角関数 分数
三角関数 分解
三角関数 部分積分
三角関数 分数 積分
三角関数 物理
三角関数 部分分数分解
三角関数 分数 微分
三角関数 分野
三角関数 分配法則
三角関数 分数 最大最小
三角関数 ベクトル
三角関数 べき乗
三角関数 勉強
三角関数 べき乗 積分
三角関数 勉強方法
三角関数 ベクトル 合成
三角関数 べき級数
三角関数 便利
三角関数 ベクトル表示
三角関数 勉強 アプリ
三角関数 ボール
三角関数 ボケ
三角関数 ボカロ
三角関数 π
三角関数 π/2
三角関数 πとは
三角関数 π/2-θ
三角関数 パラメータ
三角関数 パターン
三角関数 π 何度
三角関数 π-θ
三角関数 π 計算
三角関数 パラメータ表示
三角関数 ピタゴラスの定理
三角関数 pi/2
三角関数 ピラミッド
三角関数 pi
三角関数 ピアノ
三角関数 ピアス
三角関数 ピザ
エクセル π 三角関数
ピタゴラス数 三角関数
ピタゴラスの定理 証明 三角関数
三角関数 プログラミング
三角関数 プラスマイナス
三角関数 プリント
三角関数 プログラム
三角関数 プラスさたこ
三角関数 プロット
三角関数 プラス90度
三角関数 プラスπ
三角関数 period
perl 三角関数
三角関数 ポイント
三角関数 ポルトガル語
三角関数 グラフ ポイント
powershell 三角関数
postgresql 三角関数
povray 三角関数
三角関数 cos 合成
三角関数 いつ習う
三角関数 位相ずらし
三角関数 位相のずらし方
三角関数 因数分解
三角関数 javascript
三角関数 lim
ltspice 三角関数
ln 三角関数
三角関数 python
qt 三角関数
三角関数 とは
三角関数 vba
三角関数 vb.net
三角関数 ver
c++ 三角関数
vba 三角関数 逆関数
vb 三角関数
vb6 三角関数
vbs 三角関数
verilog 三角関数
vhdl 三角関数
三角関数 わかりやすく
三角関数 xy
三角関数 xの範囲
三角関数 x軸
三角関数 x軸対称
三角関数 x軸 y軸
三角関数 0≦θ 2π
三角関数 0度
三角関数 0以上π/2以下
三角関数 0≦θ 2π 方程式
三角関数 180-θ
三角関数 15度
三角関数 1
三角関数 1a
三角関数 120度
三角関数 1+tan^2θ=1/cos^2θ
三角関数 1/2
三角関数 1辺と角度
三角関数 105度
三角関数 1から
三角関数 2倍角
三角関数 2乗
三角関数 2倍角 公式
三角関数 2直線のなす角
三角関数 2π
三角関数 2θ
三角関数 2分のπ
三角関数 2分の1
三角関数 2乗 積分
三角関数 2辺
三角関数 30度
三角関数 3倍角
三角関数 3倍角の公式
三角関数 3乗
三角関数 345
三角関数 360度
三角関数 3乗 積分
三角関数 36度
三角関数 300°
三角関数 3d
三角関数 45度
三角関数 4倍角
三角関数 4乗 積分
三角関数 4乗
三角関数 4分のπ
三角関数 4分の3π
三角関数 5倍角
三角関数 5/4π
三角関数 5π
三角関数 50度
三角関数 5乗
三角関数 55度
三角関数 3 4 5 角度
三角関数 3 4 5
三角関数 π/5
三角関数 解の個数 5個
三角関数 60度
三角関数 6つ
三角関数 6分のπ
三角関数 6分の7π
三角関数 6分の11π
三角関数 6種類
三角関数 6倍角
三角関数 6分の13π
三角関数 6
11/6π 三角関数
三角関数 7倍角
三角関数 75度
三角関数 75°
三角関数 70度
三角関数 72度
三角関数 7/4π
三角関数 8/3π
三角関数 e3 80 80計算
三角関数 π/8
三角関数 e3 80 80公式
三角関数 e3 80 80問題
三角関数 90度
三角関数 90度以上
三角関数 90度-θ
三角関数 90度がない
===
    |
    |
    |
"make you feel, make you think."
SGT&BD
(Saionji General Trading & Business Development)
説明しよう!西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である!平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである!「働かざること山の如し」。彼がただのニートと違う点はたった1つだけ!そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。