
この世界は数のゲームだ。
売上も、年収も、数だ。年齢も数だ。
算数と数学の基礎を教えよう。
基本的に、数は、増えるか減るかしかない。
余談だが、英単語を覚えるのが面倒臭すぎるが故に、
- 増える(increase)
- 減る(decrease)
だけ覚えておけば、太った友人を見かけた時に、
「you seems increasing about the number of your body in 3D」
(君の3次元における君の体の数値が増えたように見える)
という無理矢理な英語で、
「太った」
という表現・単語を誤魔化せるのでは無いか、とかいう無茶苦茶なことを考えたことがあるが、実際のところ、数学の世界は、「こーゆーことを数表現でやろうとしている」に等しい。
数学とは、計量測定性、計算論理性にその特徴がある。いわば全てを数とその論理計算に還元する。「KPI野郎」みたいなもんだ。定量化したがる。
増えるには、「足し算的、掛け算的」のどちらかしかない。
減るには、「引き算的、割り算的」のどちらかしかない。
数の世界は、「1」と「0」が全てだ。
2は1+1だ。
3は1+1+1なのだ。
111111111×111111111=12345678987654321なのだ。
さらに、
1/10、1/100、1/1000…..
と分割を極限に小さくしていくこともできる。
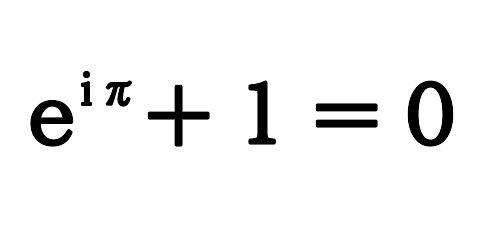
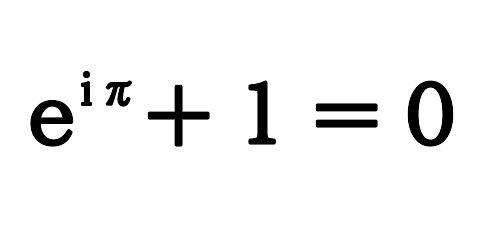

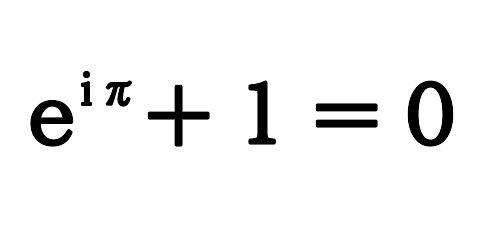
オイラーの公式には数学の主要登場人物が全て登場しており、その関係性が叙述されているから美しいとされる。
数、とは、
自然数に始まり、
マイナスへの拡張世界である整数、
1未満の分数が登場する有理数、
割れない無理数(πは無理数の登場人物)、実数と拡張されていく。
さらに実数から、「虚数・複素数」という世界へ。iはその虚数の世界の人物。
この発展の歴史は、「ある体系における矛盾を上位レイヤーで解決する」というものである。課長レベルの対立を、部長レベルで解決する、部長レベルの対立を、役員レベルで解決するという感じに近い。
ご存知の通り、正方形の対角線は√2、正立方体の立体的な対角線は√3。いわばこの微妙な数字が有理数の世界までの体系で解決できなかったからこそ「ルート」とかいう無理数の世界に手を出してきた、開拓してきたのが数学史である。
10に10をかけていくと、
10、100、1000、10000、100000….
と大きくなっていく。
よく知られたようにこれは累乗で表現されるが、累乗の場合、Base(基数)とExponent(指数)という二つの要素によって表現がなされるが(数字の右上にちょこんと数字を書くスタイル)、逆に「10000をBase何個と捉えるか?」というのはlog(対数)の捉え方である。こうすることで、掛け算を「足し算化」して簡略化できる。すなわち、baseが10であると、100は2、1000は3、10000は4になる。
「基数何個分ですか?(何回かけた分ですか?)」と問うてるので割り算のようなものである。誰かが、「対数は回数」と言っていたのがaha体験として忘れられない。
この「掛け算と、掛け算の足し算化」は、数学の中で、特に関数解析の世界でかなり重要な概念となる。例えば、「女は3回エッチすると飽きる」とか、「大抵の流行はいつか終わる」とか、「売れてた商品がやがて売れなくなる」とか、そういう現象の背後には、10→100(90up)、100→1000(900up)、1000→10000(9000up)、10000→100000(90000up)という涙ぐましい努力というのが、ただの「1、2、3、4、5・・・・」に還元されている可能性がある。
そして、この、
「何が何の掛け算で出来ているか」
という概念はルート(√)の世界に接続される。ルート(スクエアルート)は、「それがどう数の何と何の掛け算で出来ているものか」という概念であり、4のルートは2、16のルートは4である。
ルートは英語でroot。まんま。そして、square root(2乗根)、cube root(3乗根)と英語で表現することからもわかるように、幾何的な概念が頭にあるとわかりやすい。完全な余談であるが、「辺」の増え方と「面積」の増え方の関係、表面積の増え方と「体積」の増え方の関係も、ここで関連させて押さえておくと良いだろう。よく言われる、「客数」×「客単価」×「購買頻度」=売上、が、いわゆるキューブルートの関係構造にあって、立方体的なイメージを浮かべられるのが理数的センスである。
掛け算ってのは、「倍々」で効いてくるが、これは「減る」時も同じ。0.1に0.1をかけると0.01になる。物凄い勢いで減っていく。
この性質の違いによって、
- 足し算 → 多項式的
- 掛け算 → 因果論理的
になる。足し算は羅列というか横並べ的というか。これに対して、掛け算は関連していく。だから因果論理を書き表したフローチャートでの計算でも掛け算だし、条件付き確率でも掛け算が使われる。
(というか大抵の立派な数式は掛け算と割り算の羅列)
よく言われる「ボトルネック」は掛け算の途中プロセスでどこかが破綻している。
足し算の違いと掛け算の違いは、統計確率論であったり、関数モデリングの世界にまで到達しないと意外と見えてこないものであったりするが、掛け算というのは相互依存的に効いてくる。かける数とかけられる数によってかなりインパクトが変わってくる。
ボトルネックはプロセスの歩留まりとだけ考えている人間も多いが、実際のところ、「3次元が2次元になるか、1次元になるか」というような次元の違い=空間的な違いをもたらすものであったりする。掛け算というのは構成要素の数同士の相互依存が強いわけだが、これによって面積や体積を表現できるからである。また、面積や体積を考える「幾何の分野」において、「辻褄が合わない矛盾」から、ルートなりパイなりといった無理数が登場してきたことも押さえておきたい。いわば、マイナスの数にしろ、分数にしろ、ルートやパイにしろ、複素数にしろ、「なんか辻褄が合わない部分を埋め合わせる架け橋」的な役割を数学の世界においては担ってきたものと言えるが、そうやって数の体系が整備されたおかげであちこちを縦横無尽に飛び回れるのである。
足し算と掛け算の本質を理解することと同様に、
「引き算」
「割り算」
の本質を理解することもまた重要なのである。この「割り算」というのは、大抵の分析に登場する。割り算は数学的シーンでとことん登場する。何が何で割られているか、というのは、「何は何の何個分なのか(包含除)」であったり、「何は何と比べてどうなのか」というものでもあるからだ。比率、プロポーションの世界でもある。
テイラー展開などもこの割り算を究極に突き詰めたものである。割り算は解析・分析、やがて「無限」の概念へと繋がっていく。小学生レベルだと「無限」というのと、
| 単位 | 読み方 | 大きさ |
|---|---|---|
| 一 | いち | 100 |
| 十 | じゅう | 101 |
| 百 | ひゃく | 102 |
| 千 | せん | 103 |
| 万 | まん | 104 |
| 億 | おく | 108 |
| 兆 | ちょう | 1012 |
| 京 | けい、きょう | 1016 |
| 垓 | がい | 1020 |
| 秭 | じょ、し | 1024 |
| 穣 | じょう | 1028 |
| 溝 | こう | 1032 |
| 澗 | かん | 1036 |
| 正 | せい | 1040 |
| 載 | さい | 1044 |
| 極 | ごく | 1048 |
| 恒河沙 | ごうがしゃ | 1052 |
| 阿僧祇 | あそうぎ | 1056 |
| 那由他 | なゆた | 1060 |
| 不可思議 | ふかしぎ | 1064 |
| 無量大数 | むりょうたいすう | 1068 |
という増えるベクトルばかりを意識してしまうかもしれないが、実際の実務上はむしろ「減るベクトルでの無限」の方が重要だ。かなり重要だ。いわゆる微分は個々と密接に関係していることになる。テイラー展開と微分の関係性は意外と見落とされがちである。
やがて、この、「無限に分割していく」という概念は、e(ネイピア)とも接続していくことになる。ネイピアはある要素を増やしながらある要素を減らす、いわば、部屋の暖房をつけながらアイスを食う、みたいなことを突き詰めてやった先にどうなるか、何に収束していくかという話でもあるのだ。正直、拡散過程はどこまでも拡散することができるが、「減るベクトル」での収束過程というのは、やがて、「一定値に収束する」だとか、「ここから先は端折っても良くね?」という考えに辿り着き、やがてそれがapproximatelyな世界になる。近似値計算の世界にたどり着くことになる。
数の概念は、基本的にスカラーであるが、やがて「数の組」と定義された「ベクトル」の世界へと発展していく。その発展の仕方はまるでマトリョーシカ構造のようである。幾何空間における数の組とベクトルにおける数の組の違いは「座標が無いこと=位置がない」とされる。
幾何空間の世界ではユークリッド距離の定義が極めて重要なものとなる。距離というものを定義した時から、この世界での分析が始まっていく。
ここからお馴染みの因数分解の話と接続していく。
ここから線形代数という概念が浮かび上がってくる。因数分解←→展開の関係は、「その数が何と何で成り立っているのか」ということである。共通因子を括り出す=集約する=転換・変換するみたいな話はよく出てくる。ペーパーテスト上では、数学という学問はほぼほぼこの「読み換える」という作業に終始することになるだろう。それはさておき、因数分解の作業というのは、物事の二面性を見ている。いわば対称性を見ている。これは代数学・方程式分野に根底で流れる共通性である。結局、全ての数は1の足し算であるし(逆も然り)、物事は掛け算・割り算で表現できる。数の世界は全て連鎖して繋がっている。英語というのが、「ストーリーと論理及び英語構造、並びに文系センス又は面白さ若しくはトークスキルの本質」で触れたように基本的なパーツとその連鎖で成り立っていることと似ているように、数学もまた同様なのである。また、冒頭に述べたように、
- 自然数
- 整数
- 有利数
- 無理数
- 実数
- 虚数
というように矛盾を上位レイヤーで解決する(そのための上位レイヤーを拡張する)という歴史の積み重ねで発展してきた数学の世界では、何かしら落とし所が存在するのである。
もう少しマニアックな話をすると群論である。群論とは、集合と、その要素の積がテーマであるが、単位元、逆元、結合法則がその条件である(結合法則は順番を無視して良い、ということである。確率の組み合わせ論の世界で「順列(permutation)」に触れればわかるが順番を考慮するかしないかは極めて重要な論断である)。逆元というのは逆になる演算であり、単位元は早い話が「1」である。素となる数字である。
そもそも論、単位元、逆元、結合法則を満たすことを定義した時点で、ある程度無矛盾的にクルクルと回る、展開するのである。
===
    |
    |
    |
"make you feel, make you think."
SGT&BD
(Saionji General Trading & Business Development)
説明しよう!西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である!平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである!「働かざること山の如し」。彼がただのニートと違う点はたった1つだけ!そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。
