中卒向け、高卒向け、大卒向けのコピーライティング・マーケティング講義を行います。

 

 

中卒向け

 

稼げる仕事は、たいていの場合、中卒には手の届かないものばかりです。

職種	平均年収
医師	約1,378万円
航空機操縦士	約1,072万円
大学教授（高専含む）	約1,072万円
その他の経営・金融・保険専門職業従事者	約1,030万円
法務従事者	約945万円
大学准教授（高専含む）	約856万円
管理的職業従事者	約840万円
歯科医師	約787万円
システムコンサルタント・設計者	約734万円
研究者	約714万円
小・中学校教員	約699万円
著述家、記者、編集者	約696万円
大学講師・助教（高専含む）	約694万円
高等学校教員	約693万円
発電員、変電員	約666万円
公認会計士、税理士	約659万円
音楽家、舞台芸術家	約647万円
輸送用機器技術者	約647万円
企画事務員	約621万円
鉄道運転従事者	約615万円
電気・電子・電気通信技術者（通信ネットワーク技術者を除く）	約611万円
機械器具・通信・システム営業職業従事者（自動車を除く）	約601万円
化学技術者	約595万円
獣医師	約592万円
機械技術者	約587万円
建築技術者	約586万円
他に分類されない専門的職業従事者	約584万円
薬剤師	約581万円
金融営業従事者	約573万円
土木技術者	約567万円

https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450091&tstat=000001011429&cycle=0&tclass1=000001164106&tclass2=000001164107&tclass3=000001164111&stat_infid=000032182952&tclass4val=0

 

でも、中卒でも人生逆転できるのがコピーライティング。

中卒でも、コピーライティングで年収2000万円稼げます！！

考えてみてください。

単純計算で、10万円のセールスレターを月に10本仕上げれば100万円が稼げることになります。

 

コピーライティングとは何か？

それは、CVR（成約率）を高める技術です。

 

アクセスに対して、実際に買ってくれるお客さん（＝成約してくれるお客さん）の割合をCVR（＝成約率）と言います。

CVRを高めると、アクセスあたりの成約が良くなります。

よって、多くの事業者は、

反応が取れるコピーライター

を求めています。

 

コピーライティングは実力主義の世界です。

学歴は関係ありません。

売れるコピーを書ければそれで良いのです。

 

また、シンガーソングライターのように、印税収入を得ることもできます。

セールスレターの仕事を受注して、書いて納品するスタイルも良いですが、自分で売れるセールスレターを書いて保有して、そこから発生する売上で印税収入を得続けることもできます。

売り物はアフィリエイトリンクでも良いし、自分の商品でも良いのです。

 

コピーライティングは売る力です。

売る力があれば、会社に雇われずに自分のペースで自由に生きていけます。

現代最強のスキルです。

 

セールスマンシップインプリント。

印刷されたセールスマンが、あなたが寝ている間にも勝手に営業をして、不労所得をもたらしてくれる。

これがコピーライティングの素晴らしさです。

 

 

高卒向け

 

コピーライティングの素晴らしさは、複利曲線にあります。

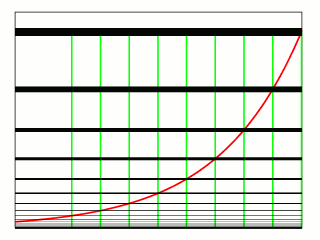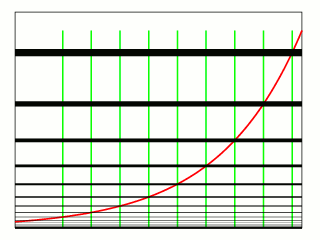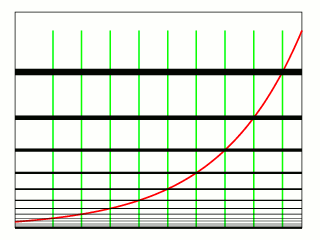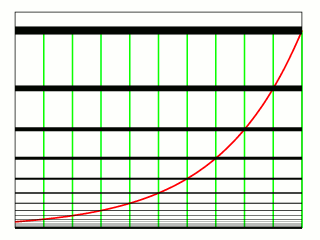
アクセスを成約し、成約から得られた報酬をアクセスに再投資する、これを繰り返すことによって、どんどんお金が増えていくのです。

アクセスを金で買い、一部を成約させ、発生した報酬の一部をアクセスを得るために再投資する。

このサイクルを何回も回した時、成約率0.5%の違いがとんでもない違いを生みます。

サイクル回数	成約率1％の収益	成約率0.5％の収益
0	0円	0円
1	5,000円	2,500円
2	12,500円	6,250円
3	25,625円	12,813円
4	51,031円	25,516円
5	101,566円	50,783円
6	202,882円	101,441円
7	405,911円	202,956円
8	811,776円	405,888円
9	1,621,289円	810,577円
10	3,237,922円	1,620,906円

お金持ち本や自己啓発本のみならず、数学の本にも書いてある、

人類最大の発明である複利を味方にしろ！

というのはまさにコピーライティング・マーケティングのことなのです。

サイクル	成約率 1% 収益	成約率 0.5% 収益
1	5,000 円	2,500 円
2	12,500 円	6,250 円
3	31,250 円	15,625 円
4	78,125 円	39,063 円
5	195,313 円	97,656 円
10	12,207,031 円	5,103,515 円
15	3,051,757,813 円	759,887,695 円
20	762,939,453,125 円	189,819,726,563 円
25	190,734,863,281,250 円	94,909,431,640,625 円

要するにこれは、

一次関数的な努力ではなく、二次関数的な努力をしようね

ということなのです。

報われる努力というのは、レバレッジが効く努力です。

 

朝起きて、

会社に行き、

働いて、

電車に揺られて帰って・・・・

ということは自分の限られた時間と労力の切り売りなのです。

 

しかも、これは税金対策にもなります。

Vanessaezekowitz at English Wikipedia, CC BY 3.0 <https://creativecommons.org/licenses/by/3.0>, via Wikimedia Commons

 

ラッファー曲線と言って、政治家が参考にしている数理モデルがあるのですが、税率を上げすぎると国民が働くなって徴収金額が落ち、税率を下げすぎると税金が少なくなるので、ちょうど良い塩梅を目指そう、というものです。支配者はこんなことを考えながら税金設定をしています。

ただこれ、

働かない選択肢がない人たちに対しては、税率をいくら上げても税金を搾り取れる

ということでもあります。

具体的にいえばサラリーマンです。サラリーマンには働かないという選択肢がないので、サラリーマンはとことん税率を上げて搾り取っても最後の最後までいける、というのが支配者の論理です。

（資本家は逃げたり節税したり、仕事をセーブします）

 

落ち目の国で平均的サラリーマンやっている以上、とことん搾り取られて、とことん疲弊するということです。

 

実際、娑婆を見てみると、法人や資本家に対して税優遇が進む一方で一般労働者に対しては締め付けが厳しくなっていたりすることがわかるでしょう。

 

働いた金から税金が取られる以上、

• いかにして働かずに金を得るか
• いかにして努力にレバレッジをかけて金を得るか

ということは極めて重要になります。

 

 

大卒向け

 

そもそも、ビジネスというのは複数の要素が複雑に絡み合う難解な世界です。しかし、そんな複雑な世界において、「シンプルな形に近似できる」というのがコピーライティングの利点でもあります。

ただし、

• 部分と全体は異なる
• 部分でできたことを全体にスケーリングできるとは限らない
• 曲線は部分で線形近似できるが、部分で直線だからと言って全体で直線とは限らない

というような、「数学の深淵」みたいな話が出てきます。

 

国家指導者の殺人数に序列をつけると、

毛沢東　＞　スターリン　＞　ヒトラー

となり、ホロコーストで大量殺人イメージのあるヒトラーが案外それほどでもない事実が浮かび上がるのですが、このようなソートをしたときに疑問に思うのは、

そもそも毛沢東率いる中国は人口が多かっただけではないか？

という疑問です。ヒトラーが率いていたドイツより、スターリンのソ連、毛沢東の中国の方が人が多そうな感じがします。

実際、「殺人の人口比」で見ると、彼ら３人はトップのランキングから脱落して、上位にはポルポトなんかが上がってきます。比率で見ると話はまた異なるわけです。

 

ここに、スケーリング・比率の問題が出てきます。

小さな規模で回っていた特定の構造は、そのまま大きな規模に拡大しても延長されるのか？という問題です。

果たして、「ある投資元本に対して、あるリターン％が投資元本に組み込まれて、さらにそこからリターンが生まれて・・・・」というような複利というのは、現実問題、スケールするのでしょうか。

 

現実問題、これは難しいのです。

投資の例で考えてみましょう。

ウォーレンバフェットの投資リターンを見ると、リターン率が最も良かったのは若かった頃で、なぜかというと、「資産規模・投資規模が大きくなっているため投資先が見つからない」という問題に面しているからです。例えば、もし株価が10倍になる企業を見つけたとしても、その企業の時価総額が10億ドルしかなかった場合、10倍になっても100億ドルで、バークシャーの運用資産にとって、3%の影響しかありません。20%の利回りを得るためには、1年で10倍に値上がりする株を、毎年7社見つけないといけないことになります。これは非現実的です。このように運用資産が巨大になると、時価総額の大きな大企業に投資しないといけないのですが、そういう企業はみんなが注目していて割高になっているので、バフェットお得意の「バリュー投資（お買い得投資）」ができなくなる、わけです。

複利カーブは理論的には美しいですが、現実問題、それを実行しようと思うと大抵の場合、問題が起こります。金融マーケットは定期的にクラッシュが起こるので、それを避けられないと財産の多くを毀損することもありますし、アメリカの大恐慌の時のように25年株価が元に戻らないなんていう地獄のフェーズもあるわけです。

 

コピーライティング・マーケティングにおいても、実際問題、複利を回そうと思うと、「やがて反応率が悪い層にあたる」とか、「マーケットが枯渇する」とか、「広告単価が上がる」などして、理想的な複利上昇カーブをサステナブルに持続することは困難になることがあります。

金融クラッシュ的に市場が落ち込んだり、流行りのメディアが変わったりするような地殻変動的な現象も起こり得ます。

 

急いで子供が欲しいからと言って9人妊娠させたところですぐ親になれるわけではない

というのはバフェットの名言ですが、この名言には数学上の重要な定数である「e（ネイピア数）」に対する本質的な問いが込められています。

1年で特定の利率がつくとした場合、これを半年にして利率を倍にする、さらに半年の半分にして利率をまたさらに倍にする・・・・ということを続けるとどうなるかという話がありますが、これはご存知のように収束していくことになります。

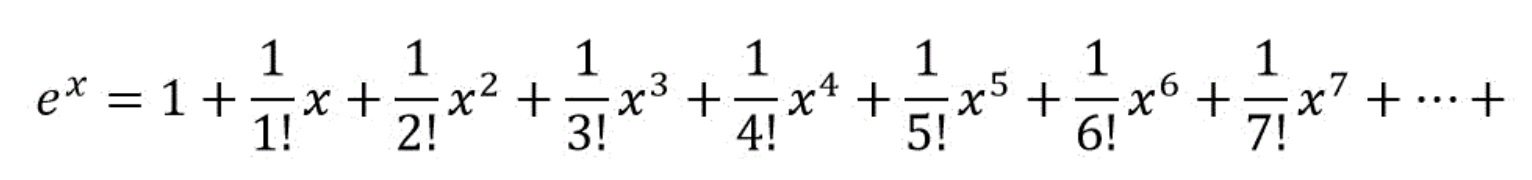
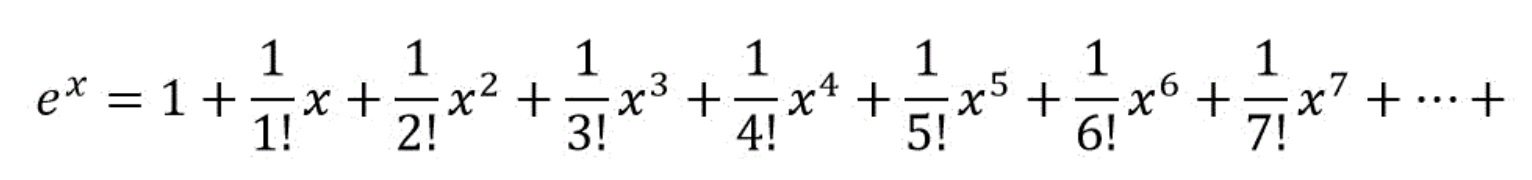
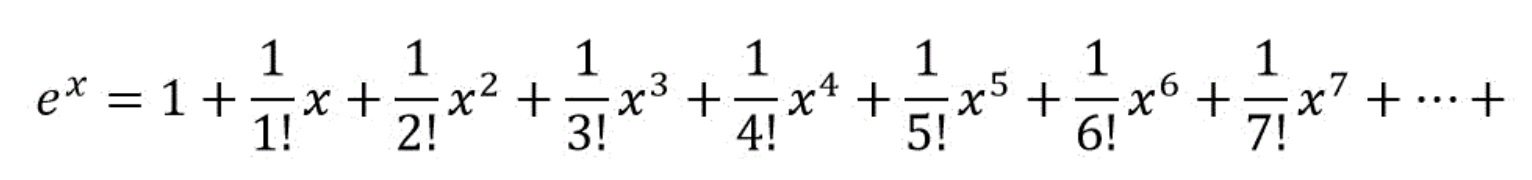
ちなみに、sinxやcosxのマクローリン展開はこれと似たような形で±を途中途中で挟み込むような感じなのですが、いずれにせよ言えることは、

増え続けるわけではない

ということです。

いわば、こういった定数的な制約がこの世界には溢れかえっています。

マクローリン展開とテイラー展開は、関数を無限の項によって近似的に表現する手法ですが、その違いは展開の中心点にあります。マクローリン展開: マクローリン展開は、関数を0の周りで展開する方法です。具体的には、ある関数f(x)をその導関数を用いて以下のように近似的に表現します。

f(x) ≈ f(0) + f'(0)x + f''(0)x^2/2! + f'''(0)x^3/3! + ...

ここで、f(0)は関数f(x)のx = 0での値です。この展開は、関数が0の周りで比較的単純な形になる場合に有用です。

テイラー展開: テイラー展開は、関数を任意の点aの周りで展開する方法です。マクローリン展開はテイラー展開の特別なケースであり、a = 0の場合です。一般的なテイラー展開は以下のようになります。

f(x) ≈ f(a) + f'(a)(x - a) + f''(a)(x - a)^2/2! + f'''(a)(x - a)^3/3! + ...

ここで、f(a)は関数f(x)のx = aでの値です。テイラー展開は、関数が任意の点aの周りで展開されるため、より一般的な場面で使用されます。

要するに、マクローリン展開はテイラー展開の特殊なケースであり、テイラー展開は関数を任意の点で展開する一般的な方法です。

 

この、

1. 投資
2. 回転数
3. リターン

の考え方はビジネスにおいてはかなり普遍的な考えで、例えば「スループット」「在庫回転率」「交差比率」というような概念で捉えられています。例えば、粗利が高い商材であるが回転率が悪い（出が悪い）ケースと、粗利が低い商材で回転率が良いケースだとどっちが儲かるか、みたいな話が出てくるわけです。

そしてこれは、「 LUXEM　DNA 」でもお話した、

新規客拡大と既存客掘り下げはどちらが有利か？

みたいな話にも繋がってきたりするわけです。

一人当たりのユーザーの可処分所得が決まっていて（定数）、購買確率がポアソン分布していて、その集合として捉えるのであれば垂直展開よりも水平展開の方が儲かると算盤を弾くのはその通りですが、それでは「ユーラシア大陸を制圧する」と息巻いて消耗していった過去の国々と同じ過ちを犯してしまう可能性があります（poduxury city voice参照）。ポテンシャルの拡大と、現実問題としての実行可能性の拡大はまた別の話です。

極端な話、一人の客からの獲得金額を10倍にするより、新規水平拡大を10倍にする方が簡単であればそうした方が良いし、逆なら縦に掘った方が良いでしょうが、いずれにせよ競争というファクター、コストというファクターもあります。

 

どこに伸び代、勝ち筋があるか？

を精緻に判断して、特定していかないといけない。複利カーブの重要性はその通りですが、フランチャイズ展開のように直線的に拡大複生産ができることには限界があるわけです。ある時・あるケースで通用したワンパッケージ・ワンセットをそのままスケーリングして使い続けられるか、それにサステナビリティがあるかというのはまた別の話なのです。

 

ビジネスのスケーリングの歴史を参照すると、スケーリングアップが継続的に続いてきたビジネスというのは、買収したり、コングロマリット化したり、新しい事業に手を出しているものなのです。

構造的限界を超えるためには、業態・業界・需給の限界を構造的飛躍によって乗り越えていかなければなりません。

 

一方で、楽天モバイルの事例のように、構造的飛躍を狙ったがゆえの危機というケースもあるわけです。

 

 

＝＝＝

＠西園寺貴文（憧れはゴルゴ13）#+6σの男

   

"make you feel, make you think."

 

SGT&BD
(Saionji General Trading & Business Development)

新たなるハイクラスエリート層はここから生まれる          




Lose Yourself , Change Yourself.（変えることのできるものについて、それを変えるだけの勇気を我らに与えたまえ。変えることのできないものについては、それを受け入れられる冷静さを与えたまえ。そして、変えることのできるものと、変えることのできないものとを、見分ける知恵を与えたまえ。） 

説明しよう！西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である！平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである！「働かざること山の如し」。彼がただのニートと違う点はたった１つだけ！そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。