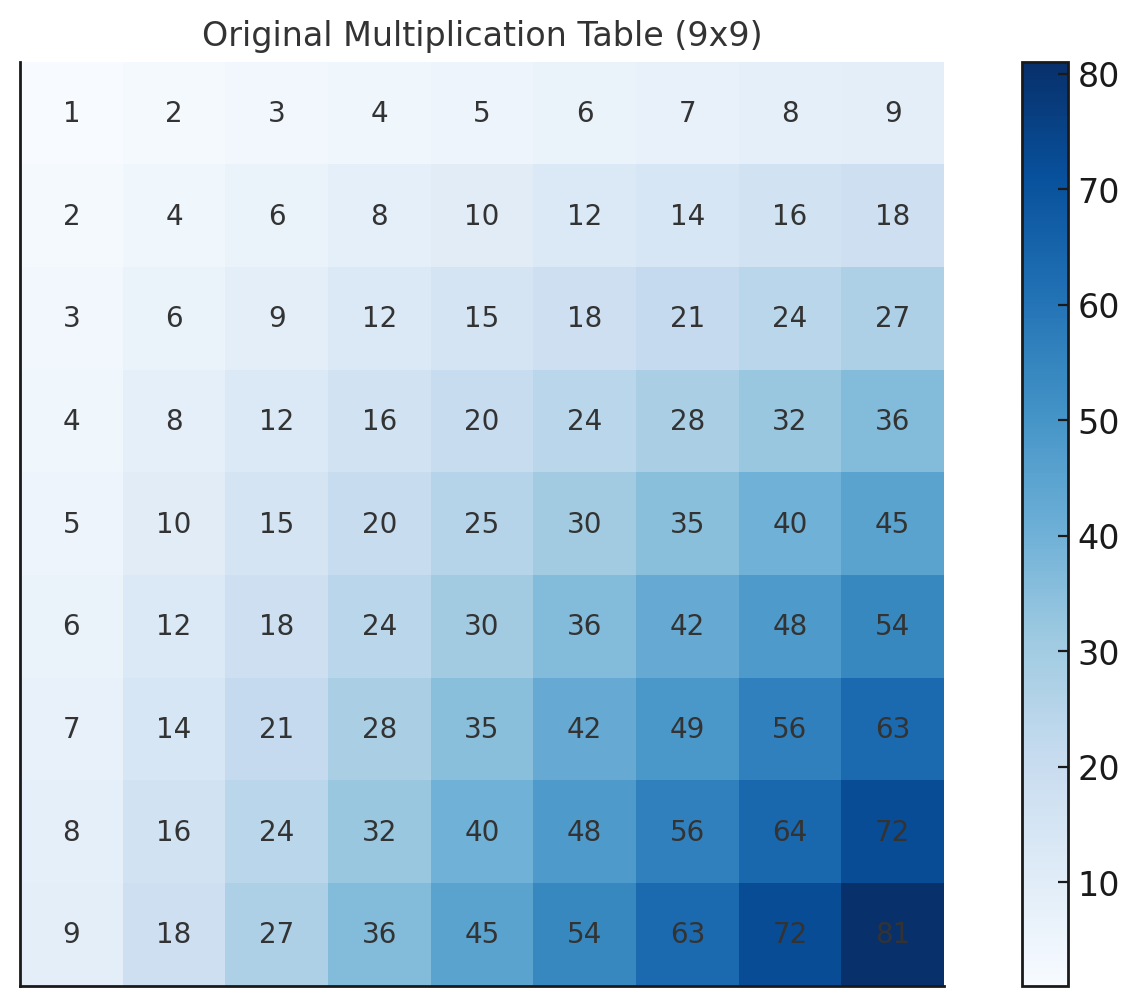
ここに九九表がある。
整然として綺麗に並んでいる。
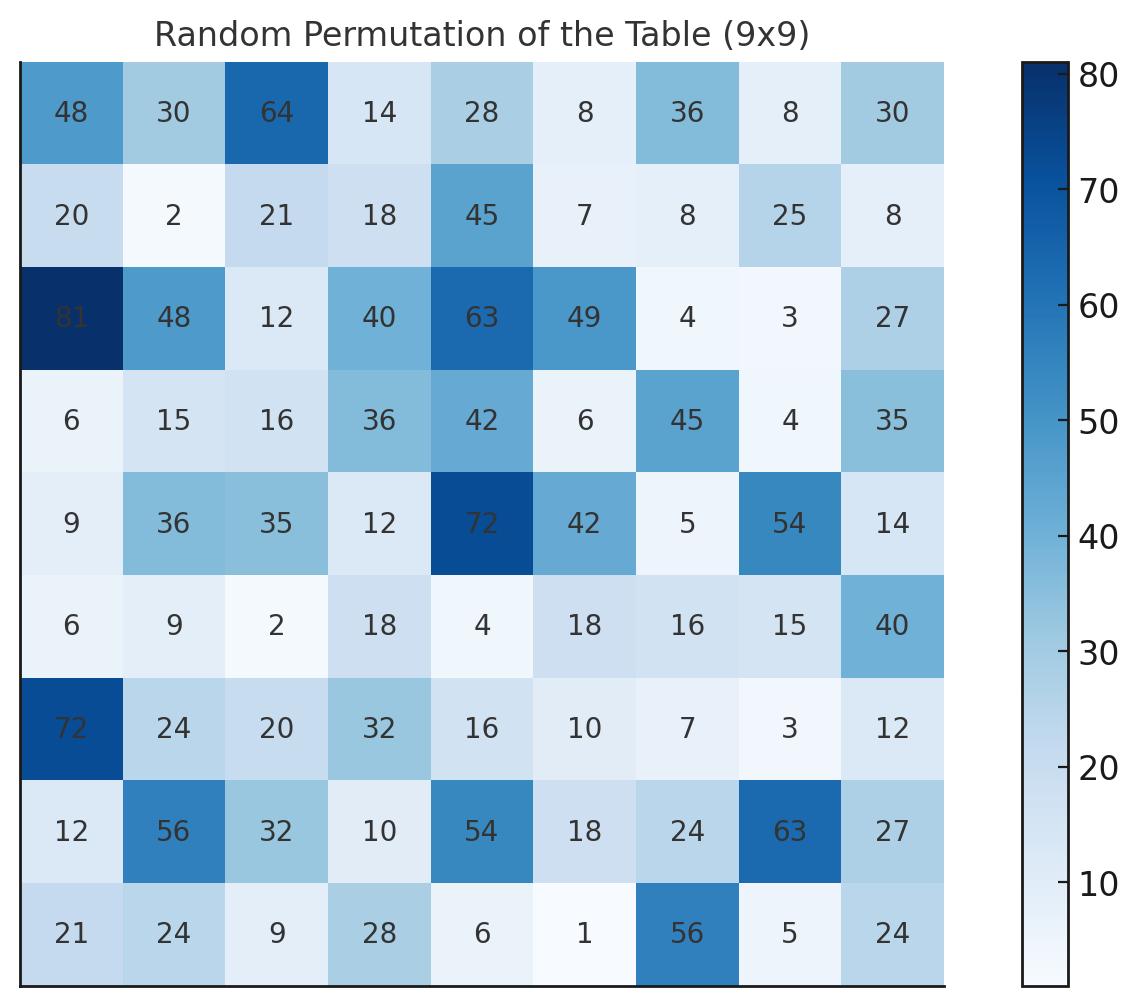



では、こうやってめちゃくちゃに並べ変えたらどうか?
多分、下の表から先に見せられると、
それが九九の表だとはわからない。
我々プロマーケター・データサイエンティストは、
常にデータを見ているのだが、
データが雑然としていて法則性が見えない場合と度々出くわす。
その際に、そこから法則性を抜き出したい。
分解したい。
・・・・・さて、この雑多な表から何を抜き出す?
そういうことなのだ。
ちなみに結論から言ってしまうと、
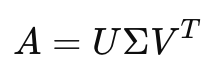 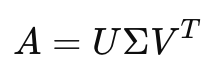  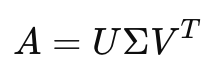 |
||||
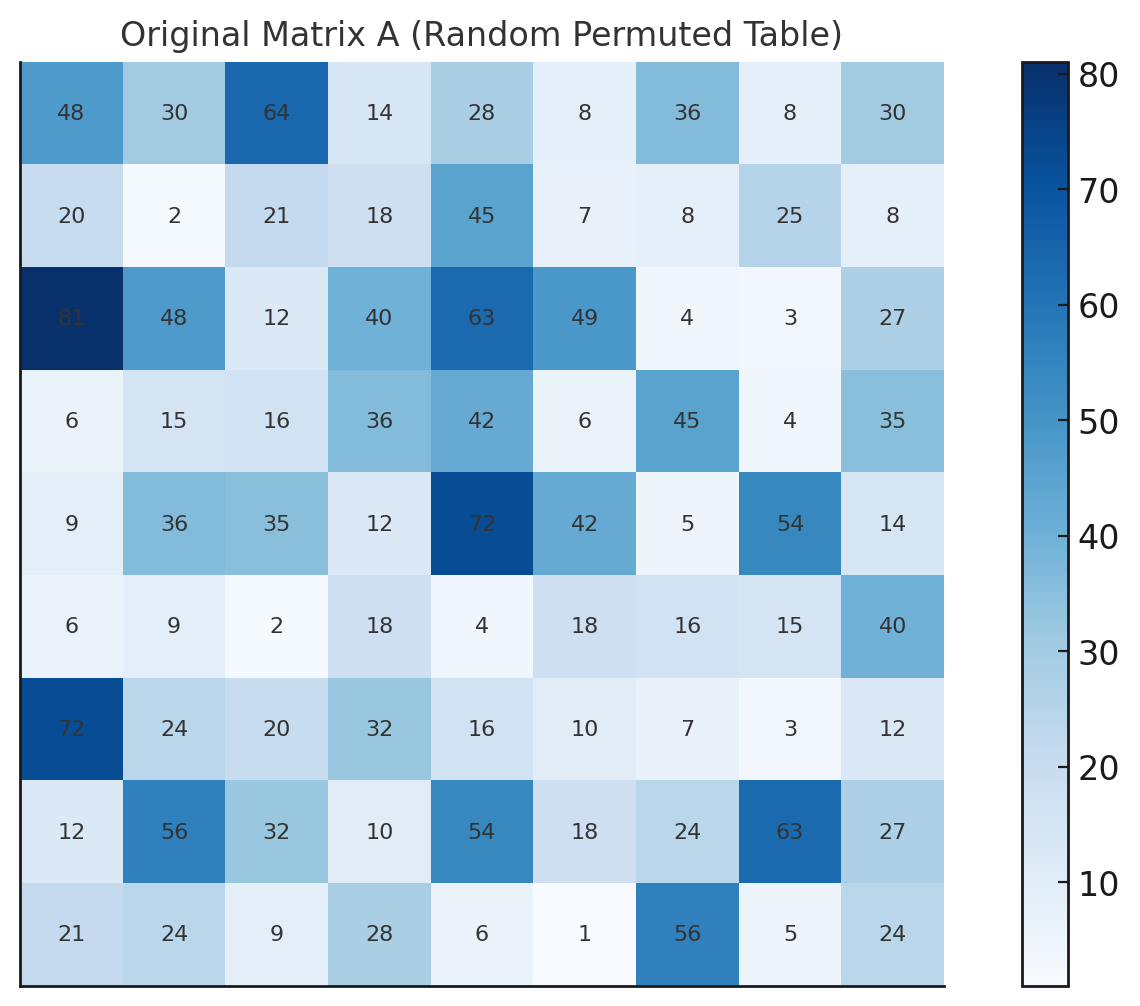    |
= | 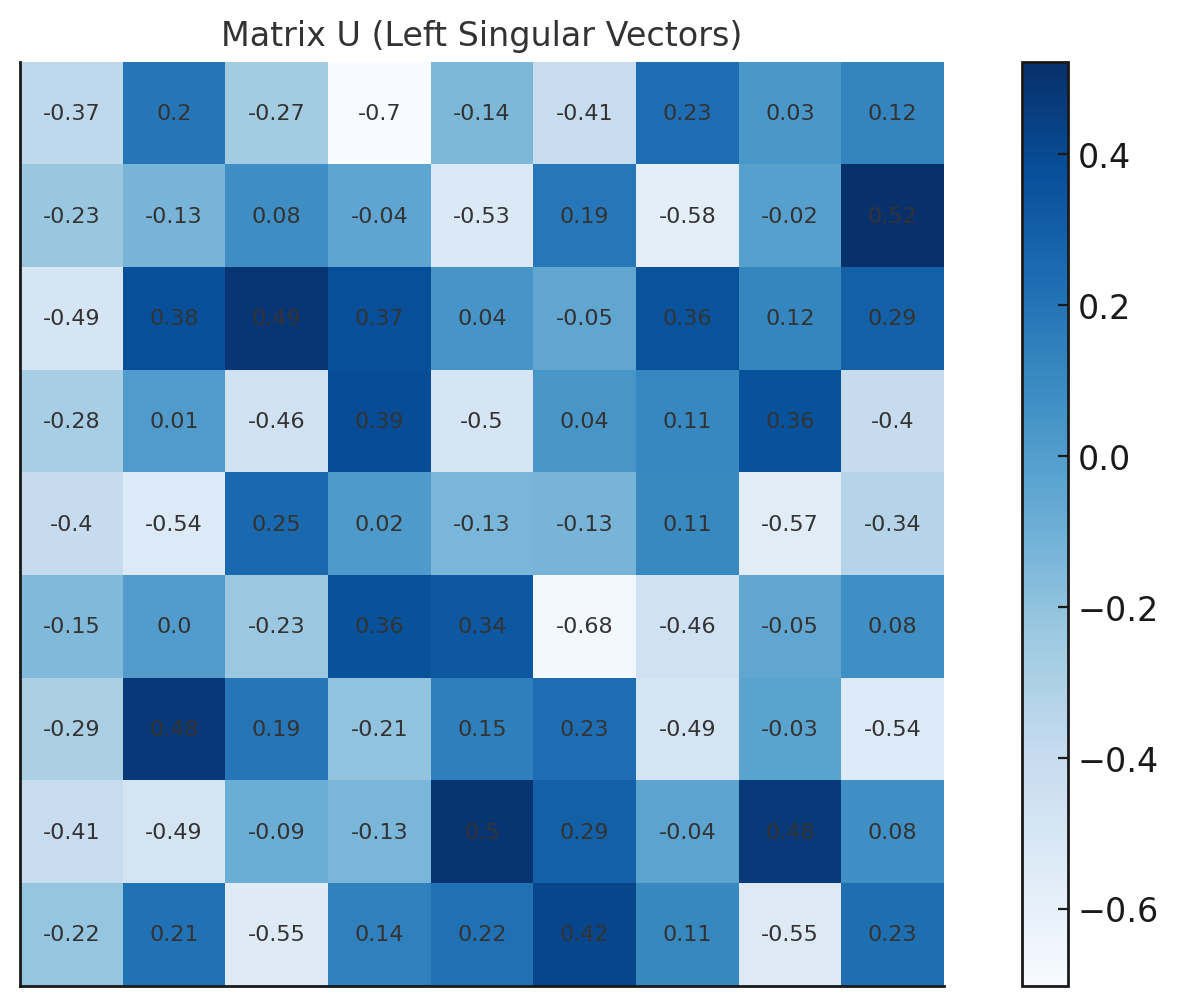    |
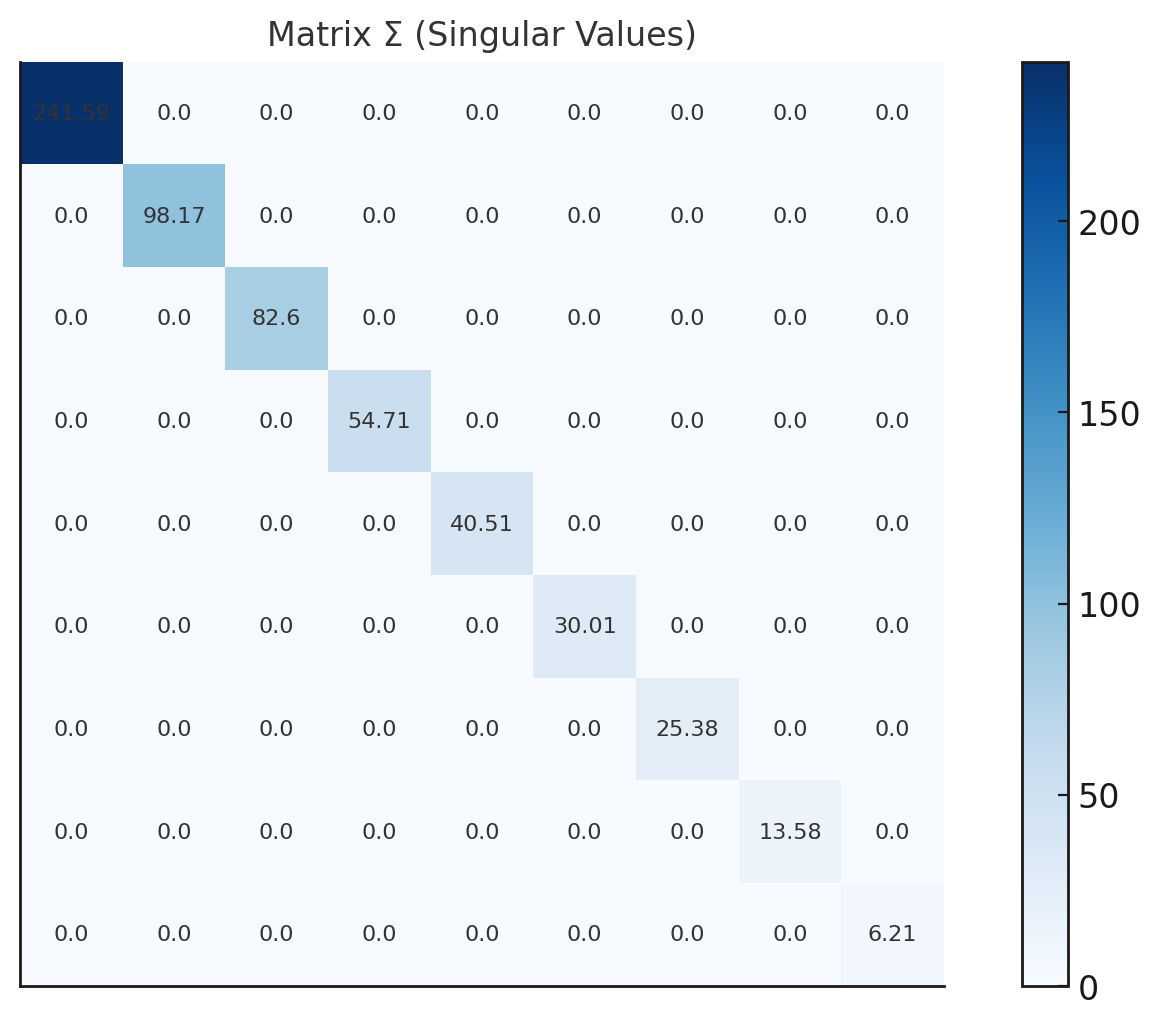    |
    |
みたいなことである。
これが特異値分解だ。
特異値分解(SVD)とは?
特異値分解(SVD:Singular Value Decomposition)は、行列を分解して、その行列の重要な特徴を抜き出す方法です。行列というのは、数字が並んだ表のようなものです。SVDは、特に大きなデータの背後に隠れている「パターン」や「関係性」を見つけるために使います。
SVDのイメージ
例を使って考えましょう。
例:学校の成績表
たとえば、学校のテストの成績表があるとします。この表には、行が「生徒」、列が「教科」の成績が入っています。例えば、次のような表です。
| 数学 | 英語 | 理科 | |
|---|---|---|---|
| 生徒A | 80 | 70 | 85 |
| 生徒B | 75 | 65 | 80 |
| 生徒C | 90 | 80 | 90 |
この成績表は3人の生徒と3つの教科があり、全体の傾向やパターンを見つけることができるかもしれません。
SVDを使うと、この表を3つの部分に分解できます:
- 行の特徴(生徒の特徴): 生徒がどんな成績のパターンを持っているか。
- 重要なパターンの強さ: 全体でどんな成績のパターンが強く出ているか。
- 列の特徴(教科の特徴): 教科ごとにどういう成績の違いがあるか。




主にこれは、多変量解析と呼ばれる分野だ。
特にコレスポンデンス分析と言われる。
そこで、線形代数(特異値分解)が使われる。
マーケティングでよく見るポジショニングマップはコレスポンデンス分析!
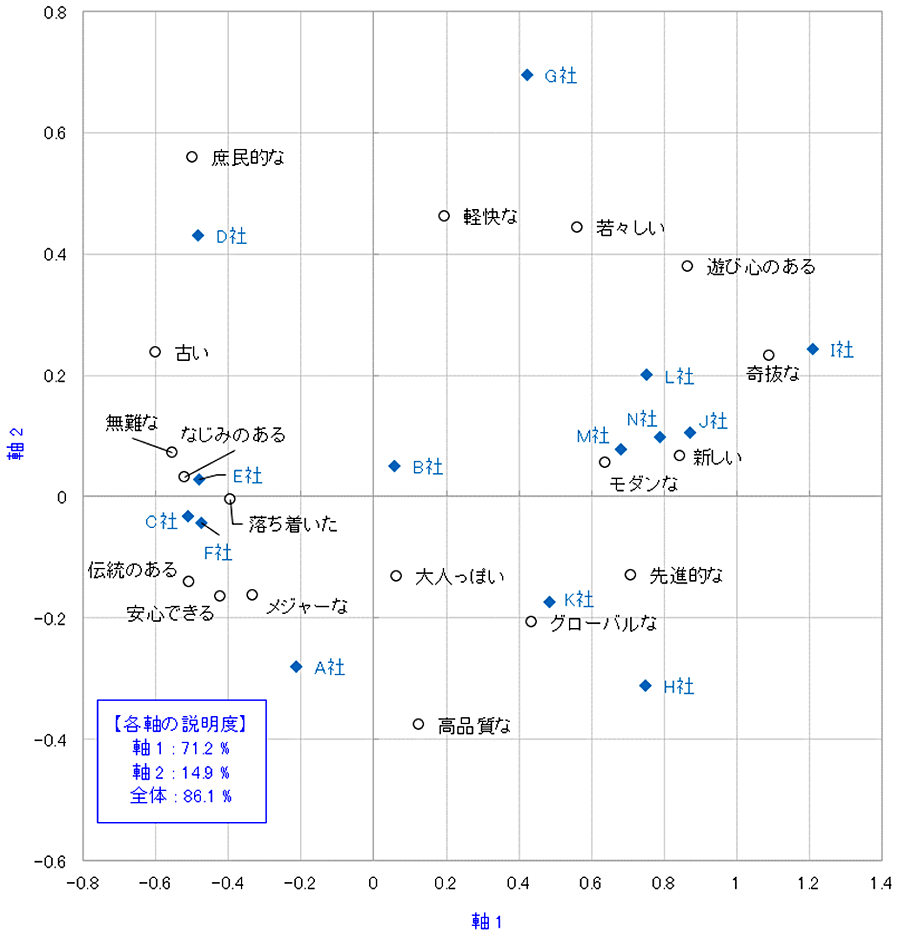



https://www.macromill.com/tabulation/faq/09-multivariate/correspondence-analysis/




コレスポンデンス分析(CA)におけるステップ2以降をより分かりやすく噛み砕いて説明します。
ステップ1:データ行列の標準化
まず、クロス集計表のようなカテゴリデータがあります。行と列の間の頻度データを扱っています。例えば、アンケート調査で「性別」と「職業」のクロス集計表があったとします。
ステップ2:行列の標準化と中心化
**「標準化」と「中心化」**は少し数学的に感じるかもしれませんが、実はこれらは単にデータを整理し、重要な部分を強調するためのプロセスです。
1. 行と列のプロファイルを作る
- まず、行と列の合計を計算し、それを基に「どの行が全体の中でどれくらい占めているか」「どの列が全体の中でどれくらい占めているか」を見ます。これは**「行と列のマージナル分布(周辺分布)」**と呼ばれます。
2. 行列の中心化
- 次に、データ行列全体を、独立モデルと呼ばれる「行と列の要素が無関係だと仮定した場合の値」からの偏差を見るように変換します。つまり、元のデータ行列から「期待される無関係な分布」を引いていきます。これにより、行と列の間に実際の相関や偏差がどこにあるのかが分かりやすくなります。
ステップ3:特異値分解(SVD)の適用
この「中心化されたデータ行列」に対して、**特異値分解(SVD)**を行います。
特異値分解とは、データ行列を3つの部分に分ける方法です:
- 行列 U: 行のパターンを抽出します。これは、行方向の「強さ」や特徴を示しています。具体的には、「どの行が他の行と比べて特徴的か」「行のパターンがどう分布しているか」を表します。
- 行列 Σ: 特異値を対角線上に持つ行列で、データ全体に対してどのパターンが重要か(つまり、行と列のどの関係が強いか)を示しています。値が大きいほど、その方向がデータにおいて重要であることを示します。
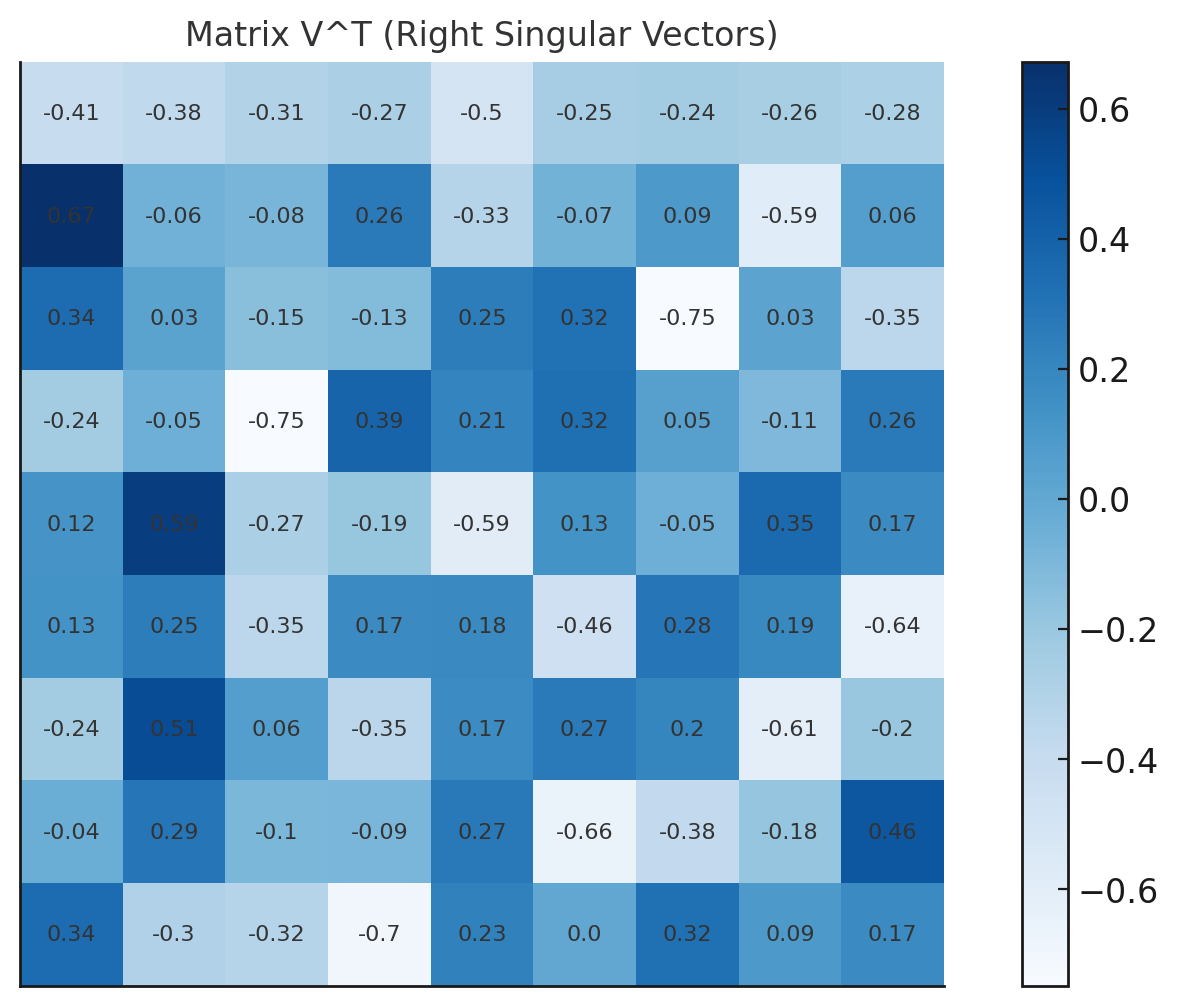
- 行列 V^T: 列のパターンを抽出します。これは、列方向の「強さ」や特徴を示しています。
ステップ4:低次元空間に圧縮
SVDによって分解された結果を基に、元のデータを低次元(通常2次元や3次元)に圧縮します。これにより、行と列の関連性がグラフ上で視覚的に表現されます。これが、コレスポンデンス分析の主要な目的です。
具体例:
例えば、行(性別)と列(職業)が近いほど、その性別の人がその職業に多いことを意味します。反対に、離れていれば、あまり関連がないことを意味します。特異値分解は、こうした関係性を捉えるための手法であり、コレスポンデンス分析で利用されています。
まとめ
- ステップ2:データ行列の行と列の合計を基にした「プロファイル」を作成し、それを使って中心化します。
- ステップ3:SVDを用いて、データの主要なパターン(行と列の強さ)を分解します。
- ステップ4:データを低次元空間に圧縮し、行と列の関係性を可視化します。
コレスポンデンス分析では、SVDを使ってカテゴリデータの中で最も重要なパターンを抽出し、行と列の関係性を可視化します。
#
特異値分解 わかりやすく
特異値分解 主成分分析
特異値分解 例題
特異値分解 何に使う
特異値分解 やり方
特異値分解 特異値
特異値分解 証明
特異値分解 アルゴリズム
特異値分解 メリット
特異値分解 主成分分析
特異値分解 やり方
特異値分解 例題
特異値分解 次元削減
特異値分解 応用
特異値分解 最小二乗法
特異値分解 python
データサイエンスとは 簡単に
データサイエンス 大学
データサイエンス 身近な例
データサイエンス 資格
データサイエンス学部
データサイエンス 独学
データサイエンス入門
データサイエンス 講座
データサイエンス リテラシーレベル
データサイエンス リテラシー 放送大学
リテラシーレベルとは
データリテラシー 文部科学省 3つのスキル
データサイエンスリテラシー 培風館
データサイエンティスト検定
データサイエンスリテラシー 問題
データサイエンス リテラシープログラム
リテラシーレベルとは
データサイエンス 応用基礎レベル
データリテラシー 文部科学省 3つのスキル
数理データサイエンス 大学
データサイエンティスト検定
数理 データサイエンス ai教育プログラム認定制度 メリット
数理 データサイエンス ai教育プログラム 就活
数理 データサイエンスとは
===
    |
    |
    |
"make you feel, make you think."
SGT&BD
(Saionji General Trading & Business Development)
説明しよう!西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である!平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである!「働かざること山の如し」。彼がただのニートと違う点はたった1つだけ!そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。
