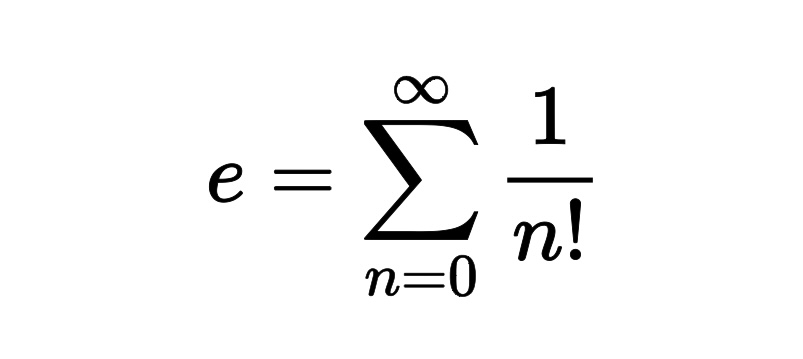I’m Eラン卒
中高で数学ほぼオール1で卒業した男が辿り着いた境地。
1:カウンティング(関数形)を理解する

文理の交差路でも触れたけど、カウンティングのセンスがまず必要。
- 1.2.3.4.5.6.7.8.9….
- 2.4.6.8.10.12.14….
- 2.4.8.16.32.64.128…
- 1.10.100.1000.10000….
- 1.1/10.1/100.1/1000….
- √2.√3.√4.√5.√6.√7.√8…..
みたいなことがパッと、頭の中でどういう増え方をするのかのイメージがつくことが極めて重要
直線的に伸びる、曲線的に伸びる、曲線的に落ち着く、みたいなもの
さらにこれを組み合わせた時にどうなるかというイメージ
あとこれもわかるとすごく良い
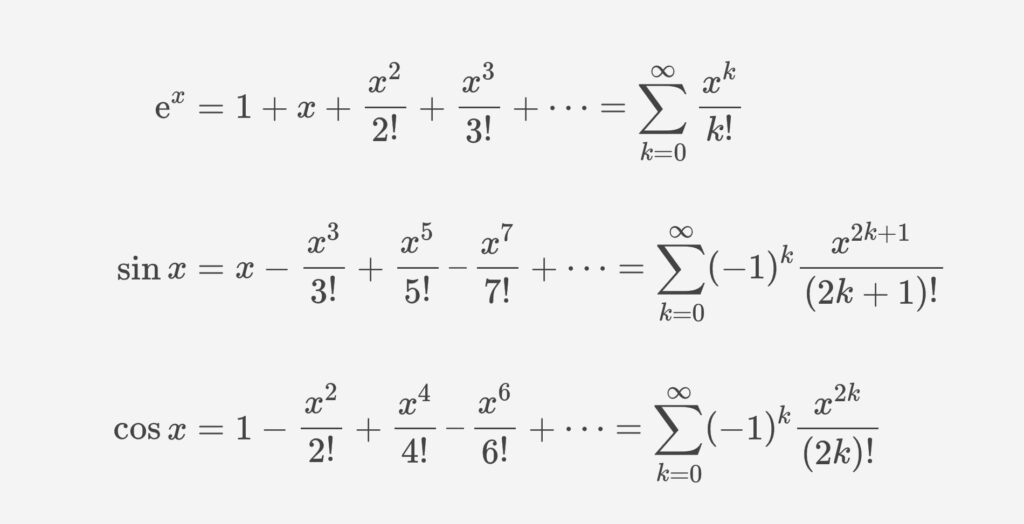
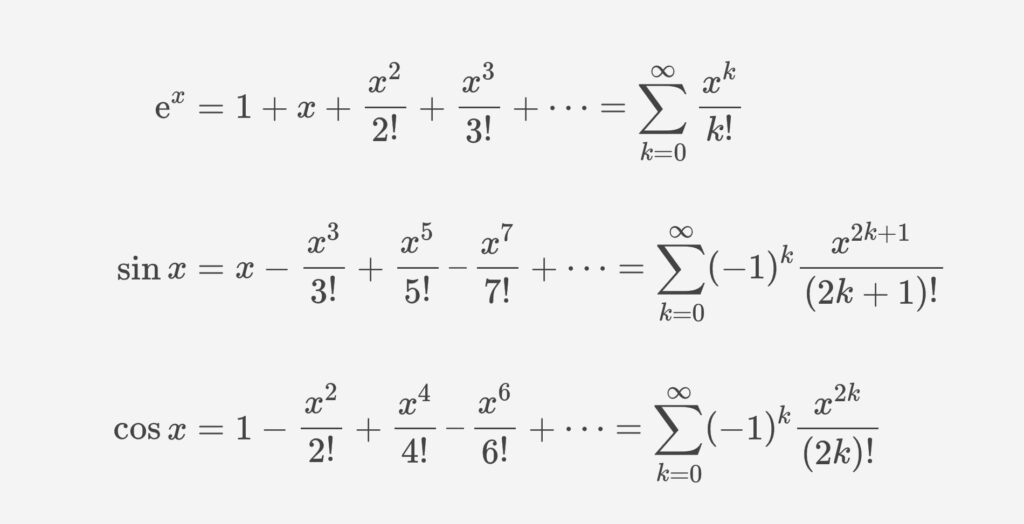

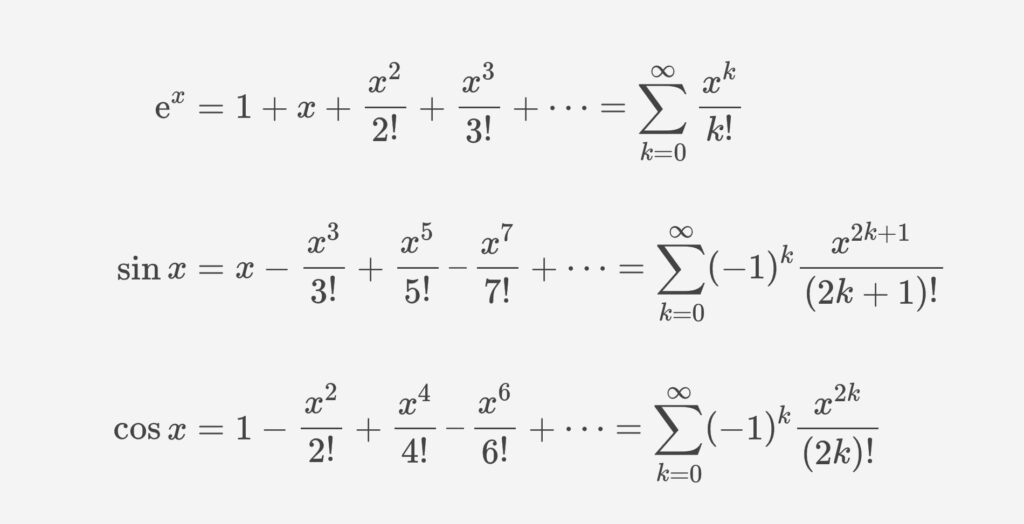
増えたり減ったり、というパターンである。
【注目エントリ】
- 天才と凡人の違いは二乗則かべき乗即か階乗則か(http://blog.livedoor.jp/nara_suimeishi/archives/51631039.html)
- 階乗関数(https://note.com/kinshati/n/nce7dbabfcaa0)
- 階乗の意味と値(https://atarimae.biz/archives/24270)
- 発散、収束、振動(https://manabitimes.jp/math/1040)
Ⅲ【媒介変数表示】2次曲線の媒介変数表示(1) pic.twitter.com/zv3NmxfMFo
— 画像でわかる高校数学bot (@easy_math_bot) August 23, 2017
2:Luxem dna 第一章を理解する
比率を理解する。何と何を比べる、ということを意識する。そしてそれは、
- 分ける
- 構成要素単位で数える
ということでもある。
林修いわく、思考は類比(アナログ)、対比(コントラスト)、因果であるが、
類比と因果は式全体で表れがちで、対比は方程式のパートの一部としてよく登場する。
だいたい、対比は
- 時間
- 確率
で使われる。時間比(where)、空間比(when)は大体鉄板パターンである。whatは数式自体がなにか(数式自体は主にwhy)、もしくは変数定数が何かであり、理系は文系と違ってwhoを考慮しない。
確率とは面積である、ということも付け加えておきたい。確率がコントラストであるということを理解しない者は永久にモンティホール問題が解けないことだろう。
ちなみに
- すごい割り算=微分
- すごいかけ算=積分
であることも付け加えておくと微分方程式や確率微分方程式への理解も深まるかもしれない。




微分方程式などは、
コントラスト = 類比対象
になっている。
動態(時間比)= 動態(類比対象)の構図である。
ちなみに、右辺と左辺の何が同じかを先に見抜くのが理解のコツである。この微分方程式ではNが連動することがわかるが、Kは定数であることがわかる。定数Kを分母にして分子Nが増大しこれが1から引かれるとはすなわちカッコ内の数字は小さくなる。小さくなった数字がNにかかるのだから小さくなる。他方、左辺におけるNは分子でありこれが大きくなるほど数としては大きくなる。増えるスピードが速いと傍で急速に減る、という図式である。
3:葛藤の構造に想いを馳せる
葛藤の構造に想いを馳せる。
例えばこういうことを考えてみる。
努力すればするほど均衡に向かっていっていないのか。poduxury 広島呉で触れたようにサチッて無いのか(saturation=飽和)。早く子供が欲しいからと9人妊娠させていないか。目盛りが意味不明な嘘くさい長期投資グラフに騙されずに、資本主義や株式市場の将来が見えるかどうか。
===
    |
    |
    |
"make you feel, make you think."
SGT&BD
(Saionji General Trading & Business Development)
説明しよう!西園寺貴文とは、常識と大衆に反逆する「社会不適合者」である!平日の昼間っからスタバでゴロゴロするかと思えば、そのまま軽いノリでソー◯をお風呂代わりに利用。挙句の果てには気分で空港に向かい、当日券でそのままどこかへ飛んでしまうという自由を履き違えたピーターパンである!「働かざること山の如し」。彼がただのニートと違う点はたった1つだけ!そう。それは「圧倒的な書く力」である。ペンは剣よりも強し。ペンを握った男の「逆転」ヒップホッパー的反逆人生。そして「ここ」は、そんな西園寺貴文の生き方を後続の者たちへと伝承する、極めてアンダーグラウンドな世界である。 U-18、厳禁。低脳、厳禁。情弱、厳禁。